题目内容
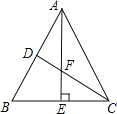
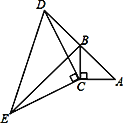
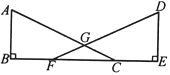
【题目】如图,点B,F,C,E在同一直线上,AC,DF相交于点G,且△ABC≌△DEF
(1)若△ABC的周长为12cm,AB=3cm,BC=4cm,求DF的长.
(2)若DE⊥BC与点E,∠A=65°,求∠AGF的度数.
【答案】(1)5;(2)50°.
【解析】
(1)由全等三角形性质,得DE=AB=3,EF=BC=4,即可求得DF的长度;
(2)由全等三角形性质,则∠D=∠A=65°,∠DFE=∠ACB=25°,有外角性质,得到∠AGF的度数.
解:(1)∵△ABC≌△DEF,
∴DE=AB=3,EF=BC=4,
∴DF=12-3-4=5;
(2)∵△ABC≌△DEF,
∴∠D=∠A=65°,∠DFE=∠ACB,
∵DE⊥BC,
∴∠E=90°,
∴∠DFE=180°-90°-65°=25°,
∴∠DFE=∠ACB=25°,
∴∠AGF=![]() .
.

练习册系列答案
相关题目