题目内容
【题目】如图,在矩形ABCD中,E是对角线BD上一点(不与点B、D重合),过点E作EF∥AB,且EF=AB,连接AE、BF、CF。
(1)若DE=DC,求证:四边形CDEF是菱形;
(2)若AB=![]() ,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为__________。
,BC=3,当四边形ABFE周长最小时,四边形CDEF的周长为__________。

【答案】(1)见解析;(2)![]()
【解析】
(1)由CD//EF,CD=EF可证四边形CDEF是平行四边形,由于DE=DC可证四边形CDEF是菱形
(2)当四边形ABFE周长最小时此时AE⊥BD,利用勾股定理可求BD、AE、ED的长度,进而求四边形CDEF的周长即可
证明:(1)在矩形ABCD中CD∥AB,CD=AB,
∵EF∥AB, EF=AB
∴CD//EF,CD=EF
∴四边形CDEF是平行四边形,
又∵DE=DC
∴四边形CDEF是菱形
(2) 在矩形ABCD中,∠BAD=90°,AD=BC=3
∴![]()
当四边形ABFE周长最小时,AE⊥BD
此时;BD=![]() ,∠AED=90°
,∠AED=90°
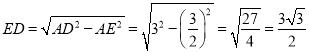
由(1)可知四边形CDEF是平行四边形
四边形CDEF的周长为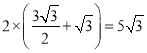
故:当四边形ABFE周长最小时,四边形CDEF的周长为![]()

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目



