题目内容
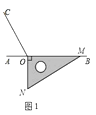
【题目】如图,以AB为直径作半圆O,点C为半圆上与A,B不重合的一动点,过点C作CD⊥AB于点D,点E与点D关于BC对称,BE与半圆交于点F,连CE.
(1)判断CE与半圆O的位置关系,并给予证明.
(2)点C在运动时,四边形OCFB的形状可变为菱形吗?若可以,猜想此时∠AOC的大小,并证明你的结论;若不可以,请说明理由.
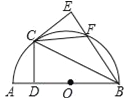
【答案】(1)CE是圆O的切线;(2)可以,此时∠AOC=60°.
【解析】
试题分析:(1)CE是圆O的切线.欲证明CE是圆O的切线,只需推知∠OCE=90°即可;
(2)可以,此时∠AOC=60°.根据已知条件可以推知△COF与△BOF为等边三角形,则四边形OCFB的四条边相等:OC=CF=FB=OB,故四边形OCFB是菱形.
试题解析:(1)解:CE是圆O的切线.理由如下:
连接OC,则OC=OB,∴∠OCB=∠OBC.
∵点E与点D关于BC对称,∴∠BCE=∠BCD.
又CD⊥AB,∴∠BCD+∠OBC=∠BCE+∠OCB=90°,即∠OCE=90°,又∵点C在半圆O上,∴CE是圆O的切线.
(2)解:可以,此时∠AOC=60°.理由如下:
连接OF.∵∠AOC=60°,∴∠OBC=∠OCB=30°.
∵点E与点D关于BC对称,∴∠CBF=∠OBC=30°,∴∠COF=60°,∴∠OBF=60°,∵OC=OF=OB,∴△COF与△BOF为等边三角形,∴OC=CF=FB=OB,∴四边形OCFB是菱形.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目