题目内容
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.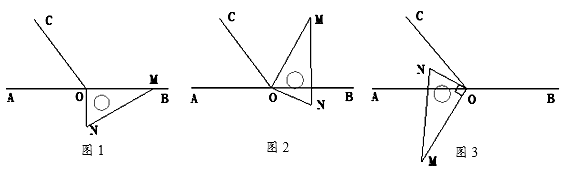
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.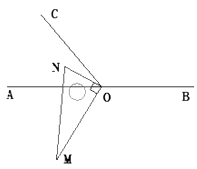
【答案】
(1)解:解:平分
理由:延长NO到D
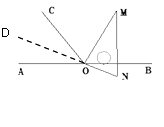
∵∠MON=90° ∴∠MOD=90°
∴∠MOB+∠NOB=90° ∠MOC+∠COD=90°
∵∠MOB=∠MOC ∴∠NOB=∠COD
∵∠NOB=∠AOD
∴ ∠COD=∠AOD
∴直线NO平分∠AOC
(2)解:t=59或14
(3)解:∠AOM-∠NOC=220
理由:∵∠AOM=90°-∠AON ∠NOC=68°-∠AON
∴∠AOM-∠NOC
=(90°-∠AON)-(68°-∠AON)
=22°
【解析】(1)利用平分线定义和等角的余角相等可证出结论;(2)须分类讨论,ON在∠AOC的内部或外部;(3)∠AOM、∠NOC都用∠AON的式子表示,二者再相减,可得出结果.
【考点精析】关于本题考查的角的平分线和余角和补角的特征,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;互余、互补是指两个角的数量关系,与两个角的位置无关才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.