题目内容
(2012•朝阳)下列说法中正确的序号有
①在Rt△ABC中,∠C=90°,CD为AB边上的中线,且CD=2,则AB=4;
②八边形的内角和度数约为1080°;
③2、3、4、3这组数据的方差为0.5;
④分式方程
=
的解为x=
;
⑤已知菱形的一个内角为60°,一条对角线为2
,则另一条对角线长为2.
①②③④
①②③④
.①在Rt△ABC中,∠C=90°,CD为AB边上的中线,且CD=2,则AB=4;
②八边形的内角和度数约为1080°;
③2、3、4、3这组数据的方差为0.5;
④分式方程
| 1 |
| x |
| 3x-1 |
| x |
| 2 |
| 3 |
⑤已知菱形的一个内角为60°,一条对角线为2
| 3 |
分析:①根据直角三角形斜边上中线性质得出即可;
②根据多边形内角和定理把8代入求出即可;
③求出平均数,再求出方差,比较即可;
④转化成整式方程,求出方程的解,进行检验即可;
⑤分为两种情况,求出对角线的长,即可判断⑤.
②根据多边形内角和定理把8代入求出即可;
③求出平均数,再求出方差,比较即可;
④转化成整式方程,求出方程的解,进行检验即可;
⑤分为两种情况,求出对角线的长,即可判断⑤.
解答:解:∵在Rt△ABC中,∠C=90°,CD为AB边上的中线,且CD=2,
∴AB=2CD=4,∴①正确;
∵八边形的内角和度数是(8-2)×180°=1080°,∴②正确;
∵平均数是
(2+3+4+3)=3,
∴方差是
[(2-3)2+(3-3)2+(4-3)2+(3-3)2]=0.5,∴③正确;
∵
=
,
去分母得:1=3x-1,
解得:x=
,
经检验x=
是原方程的解,∴④正确;

∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC,OD=OB,AB=AD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴AB=AD=BD,AB=BD=2BO,
分为两种情况:当BD=2
=AB时,BO=
,由勾股定理得:AO=3,AC=6;
当AC=2
时,AO=
,由勾股定理得:BO=1,BD=2,
∴⑤错误;
故答案为:①②③④.
∴AB=2CD=4,∴①正确;
∵八边形的内角和度数是(8-2)×180°=1080°,∴②正确;
∵平均数是
| 1 |
| 4 |
∴方差是
| 1 |
| 4 |
∵
| 1 |
| x |
| 3x-1 |
| x |
去分母得:1=3x-1,
解得:x=
| 2 |
| 3 |
经检验x=
| 2 |
| 3 |

∵四边形ABCD是菱形,
∴AC⊥BD,AO=OC,OD=OB,AB=AD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴AB=AD=BD,AB=BD=2BO,
分为两种情况:当BD=2
| 3 |
| 3 |
当AC=2
| 3 |
| 3 |
∴⑤错误;
故答案为:①②③④.
点评:本题考查了菱形的性质和判定,解分式方程、平均数、方差、勾股定理等知识点,主要考查学生的推理能力和计算能力.

练习册系列答案
相关题目
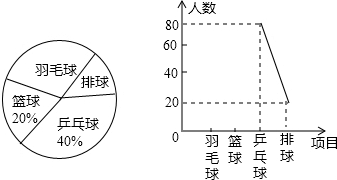 信息解答下列问题.
信息解答下列问题.