题目内容
【题目】综合与实践
问题情境
在学习了《勾股定理》和《实数》后,某班同学以“已知三角形三边的长度,求三角形面积”为主题开展了数学活动.
操作发现
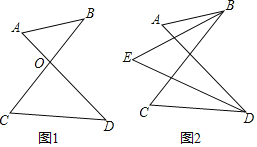
“毕达哥拉斯”小组的同学想到借助正方形网格解决问题.如图1是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C、A,他们借助此图求出了△ABC的面积.

(1)在图1中,所画的△ABC的三边长分别是AB= ,BC= ,AC= ; △ABC的面积为 .
实践探究
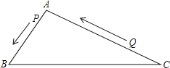
(2)在图2所示的正方形网格中画出△DEF(顶点都在格点上),使DE=![]() ,DF=
,DF=![]() , EF=
, EF=![]() ,并写出△DEF的面积.
,并写出△DEF的面积.
继续探究
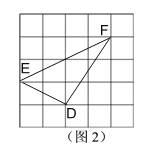
“秦九韶”小组的同学想到借助曾经阅读的数学资料: 已知三角形的三边长分别为a、b、c,求其面积,对此问题中外数学家曾经进行过深入研究.古希腊的几何学家海伦(Heron,约公元50年),在他的著作《度量》一书中,给出了求其面积的海伦公式:
![]()
我国南宋时期数学家秦九韶(约1202 ~1261),给出了著名的秦九韶公式:

(3)一个三角形的三边长依次为![]() ,
,![]() ,
,![]() ,请你从上述材料中选用适当的公式 求这个三角形的面积.(写出计算过程)
,请你从上述材料中选用适当的公式 求这个三角形的面积.(写出计算过程)
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)图见解析;△DEF的面积为4;(3)
;(2)图见解析;△DEF的面积为4;(3)![]() .
.
【解析】
(1)利用勾股定理计算△ABC的三边长;利用△ABC所在正方形的面积减去周围直角三角形的面积可求其面积;
(2)仿照“毕达哥拉斯”小组的方法利用勾股定理在正方形网格中画出△DEF,并利用割补法求其面积即可;
(3)利用秦九韶公式,代入求值即可.
解:(1)![]() ,
,![]() ,
,![]() ,
,
△ABC的面积=![]() ,
,
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)△DEF如图所示,
△DEF的面积=![]() ;
;
(3)将![]() ,
,![]() ,
,![]() 代入秦九韶公式,
代入秦九韶公式,
得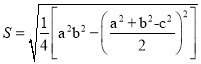
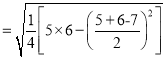
![]()
![]() .
.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案