题目内容
在平面直角坐标系中,直线AB与x轴,y轴相交于A,B两点,直线AB的函数表达式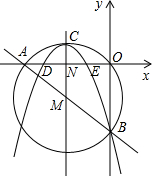 为 y=-
为 y=-
x-6,圆M经过原点O,A,B三点.
(1)求出A,B的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在⊙M上且抛物线经过点B,求此抛物线的函数解析式;
(3)如图,设(2)中求得的开口向下的抛物线交x轴于D、E两点,抛物线上是否存在点P,使得S△PDE=
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
 为 y=-
为 y=-| 3 |
| 4 |
(1)求出A,B的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在⊙M上且抛物线经过点B,求此抛物线的函数解析式;
(3)如图,设(2)中求得的开口向下的抛物线交x轴于D、E两点,抛物线上是否存在点P,使得S△PDE=
| 1 |
| 10 |
分析:(1)根据一次函数与坐标轴交点坐标求法得出答案即可;
(2)利用顶点式由B点坐标求出二次函数解析式即可;
(3)首先求出△ABC的面积,进而求出D,E坐标,进而求出△PDE的高,即可求出P点坐标.
(2)利用顶点式由B点坐标求出二次函数解析式即可;
(3)首先求出△ABC的面积,进而求出D,E坐标,进而求出△PDE的高,即可求出P点坐标.
解答:解:(1)令y=0,得0=-
x-6,
x=-8,
令x=0,y=-6,
∴A(-8,0)B(0,-6);
(2)∵CM⊥OA,
∴CM平分OA,
∵M为AB中点,
∴NM为△AOB中位线,
NM=
OB=3,
∴AM=5,
当抛物线开口向下时,顶点为C(-4,2)的抛物线解析式为:y=-
(x+4)2+2,
当抛物线开口向上时,顶点为C(-4,-8)的抛物线解析式为:y=
(x+4)2-8;
(3)∵CM=5,AD=4,DO=4,
∴S△ABC=20,
∴S△PDE=
×20=2,
令y=0,得0=-
(x+4)2+2,
D(-6,0)E(-2,0),DE=4,
×h×4=2,
h=1,
当y=1时,
1=-
(x+4)2+2,
解得:x1=-4+
,x2=-4-
.
∴P1(-4+
,1),P2(-4-
,1);
当y=-1时,
-1=-
(x+4)2+2,
解得:x=-4±
,
∴P3(-4+
,-1),P4(-4-
,-1).
故抛物线上存在点P,使得S△PDE=
S△ABC,此时,点P的坐标为:P1(-4+
,1),P2(-4-
,1),P3(-4+
,-1),P4(-4-
,-1).
| 3 |
| 4 |
x=-8,

令x=0,y=-6,
∴A(-8,0)B(0,-6);
(2)∵CM⊥OA,
∴CM平分OA,
∵M为AB中点,
∴NM为△AOB中位线,
NM=
| 1 |
| 2 |
∴AM=5,
当抛物线开口向下时,顶点为C(-4,2)的抛物线解析式为:y=-
| 1 |
| 2 |
当抛物线开口向上时,顶点为C(-4,-8)的抛物线解析式为:y=
| 1 |
| 8 |
(3)∵CM=5,AD=4,DO=4,
∴S△ABC=20,
∴S△PDE=
| 1 |
| 10 |
令y=0,得0=-
| 1 |
| 2 |
D(-6,0)E(-2,0),DE=4,
| 1 |
| 2 |
h=1,
当y=1时,
1=-
| 1 |
| 2 |
解得:x1=-4+
| 2 |
| 2 |
∴P1(-4+
| 2 |
| 2 |
当y=-1时,
-1=-
| 1 |
| 2 |
解得:x=-4±
| 6 |
∴P3(-4+
| 6 |
| 6 |
故抛物线上存在点P,使得S△PDE=
| 1 |
| 10 |
| 2 |
| 2 |
| 6 |
| 6 |
点评:此题主要考查了二次函数的综合应用以及顶点式求二次函数解析式和一元二次方程的解法,此题综合性较强,用到分类讨论思想,注意不要漏解.

练习册系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.