题目内容
如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE= ,EF⊥OD,垂足为F.
,EF⊥OD,垂足为F.
(1)求这个二次函数的解析式;
(2)求线段EF、OF的长(用含t的代数式表示);
(3)当△ECA为直角三角形时,求t的值.
(1)二次函数的解析式为:y=﹣2x2+6x+8 (2)EF= t、OF=t﹣2 (3)
t、OF=t﹣2 (3)
解析试题分析:(1)二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),
∴ ,解得
,解得 ,
,
∴这个二次函数的解析式为:y=﹣2x2+6x+8
(2)∵∠EFD=∠EDA=90°
∴∠DEF+∠EDF=90°,∠EDF+∠ODA=90°,∴∠DEF=∠ODA
∴△EDF∽△DAO
∴ .
.
∵ ,
,
∴ =
= ,
,
∴ ,∴EF=
,∴EF= t.
t.
同理 ,
,
∴DF=2,∴OF=t﹣2.
(3)∵抛物线的解析式为:y=﹣2x2+6x+8,
∴C(0,8),OC=8.
如图,过E点作EM⊥x轴于点M,则在Rt△AEM中,
∴EM=OF=t﹣2,AM=OA+AM=OA+EF=4+ t,
t,
当∠CEA=90°时,CE2+ AE2= AC2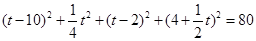

当∠ECA=90°时,
CE2+ AC2= AE2
 即点D与点C重合.
即点D与点C重合.
考点:二次函数,相似三角形,勾股定理
点评:本题考查二次函数,相似三角形,勾股定理,解答本题需要考生掌握二次函数,会用待定系数法求二次函数的解析式,熟悉相似三角形的判定方法,会判定两个三角形相似,掌握勾股定理的内容并能运用

反比例函数y= 和正比例函数y=mx的图象如图所示.由此可以得到方程
和正比例函数y=mx的图象如图所示.由此可以得到方程 =mx的实数根为( )
=mx的实数根为( )
| A.x=-2 | B.x=1 | C.x1=2,x2=-2 | D.x1=1,x2=-2 |
如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数 在第一象限内的图像与△ABC有交点,则
在第一象限内的图像与△ABC有交点,则 的取值范围是
的取值范围是
A.2≤ ≤ ≤ | B.6≤ ≤10 ≤10 | C.2≤ ≤6 ≤6 | D.2≤ ≤ ≤ |
若反比例函数y=﹣ 的图象经过点A(2,m),则m的值是( )
的图象经过点A(2,m),则m的值是( )
| A.-2 | B.2 | C.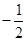 | D. |
 ,0),E(
,0),E( , 0),F(
, 0),F( ,
, ).
).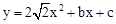 上.请你求出符合条件的抛物线解析式;
上.请你求出符合条件的抛物线解析式; 上,则可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.
上,则可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.
 经过点A(
经过点A( ,0)和点B(1,
,0)和点B(1, ),与x轴的另一个交点为C.
),与x轴的另一个交点为C. ∠MFO时,请直接写出线段BM的长.
∠MFO时,请直接写出线段BM的长.


 的顶点A(2,0),与y轴的交点为B(0,-1).
的顶点A(2,0),与y轴的交点为B(0,-1).
 经过C、B两点,与x轴的另一交点为D。
经过C、B两点,与x轴的另一交点为D。