题目内容
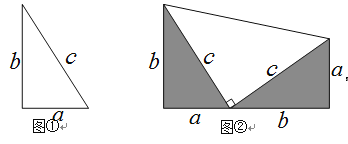
【题目】(10分)图②是一个直角梯形.该图案可以看作由2个边长为a、b、c的直角三角形(图①)和1个腰长为c的等腰直角三角形拼成。
(1)根据图②和梯形面积的不同计算方法,可以验证一个含a、b、c的等式,请你写出这个等式,并写出其推导过程;
(2)若直角三角形的边长a、b、c满足条件:a―b=1, ab=4.试求出c的值。
【答案】(1)见解析;(2)3
【解析】试题分析:(1)图②可以看做梯形,其面积为![]() (a+b)×(a+b),图②也可以看做三个直角三角形构成的,其面积为
(a+b)×(a+b),图②也可以看做三个直角三角形构成的,其面积为![]() ab·2+
ab·2+![]() c2,由此可以建立等式,然后化简即可得出结论;
c2,由此可以建立等式,然后化简即可得出结论;
(2)根据(1)中结论,将a2+b2变形为(a-b)2+2ab,然后将a-b=1,ab=4代入即可求出c的值.
试题解析:
解:(1)这个等式为: ![]()
梯形的面积可表示为 ![]()
或![]()
∴![]()
即 ![]()
(2)由(1)中的关系式![]() ,且
,且![]() ,得
,得
![]()
![]()
∵ a-b=1,ab=4,
∴![]() .
.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目