Question

【题目】已知：如图，在□ABCD中，线段EF分别交AD、AC、BC于点E、O、F，EF⊥AC，AO=CO．

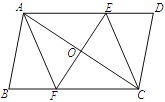
（1）求证：△AOE≌△COF；

（2）在本题的已知条件中，有一个条件如果去掉，并不影响（1）的证明，你认为这个多余的条件是 （直接写出这个条件）．

Answer 1

【答案】（1）证明见解析；（2）EF⊥AC．

【解析】

试题分析：此题主要考查了平行四边形的性质，以及全等三角形的判定和性质，关键是掌握平行四边形的对边相等；平行四边形的对角相等.

（1）首先根据平行四边形的性质可得AB=CD，∠B=∠D，AD=BC，AD∥BC，然后证明△AOE≌△COF，可得CF=AE，再证明DE=BF，进而可证明△ABF≌△CDE；

（2）在证明△AOE≌△COF的过程中，只需要∠AOE=∠FOC，对顶角相等即可，无需垂直，因此EF⊥AC是多余条件.

试题解析：（1）∵四边形ABCD是平行四边形，

∴AD∥BC．

∴∠EAO=∠FCO，

又∵∠AOE=∠COF，AO=CO，

∴△AOE≌△COF；

（2）EF⊥AC．