题目内容
等腰三角形一腰上的高等于这腰的一半,则这个等腰三角形的顶角等于( )
分析:分为两种情况:①高BD在△ABC内时,根据含30度角的直角三角形性质求出即可;②高CD在△ABC外时,求出∠DAC,根据平角的定义求出∠BAC即可.
解答:解:①如图,
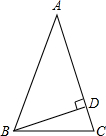
∵BD是△ABC的高,AB=AC,BD=
AB,
∴∠A=30°,
②如图,
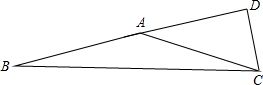
∵CD是△ABC边BA 上的高,DC=
AC,
∴∠DAC=30°,
∴∠BAC=180°-30°=150°,
综上所述,这个等腰三角形的顶角等于30°或150°.
故选:C.

∵BD是△ABC的高,AB=AC,BD=
| 1 |
| 2 |
∴∠A=30°,
②如图,

∵CD是△ABC边BA 上的高,DC=
| 1 |
| 2 |
∴∠DAC=30°,
∴∠BAC=180°-30°=150°,
综上所述,这个等腰三角形的顶角等于30°或150°.
故选:C.
点评:本题考查了等腰三角形性质和含30度角的直角三角形性质的应用,主要考查学生能否求出符合条件的所有情况,注意:一定要分类讨论.

练习册系列答案
相关题目