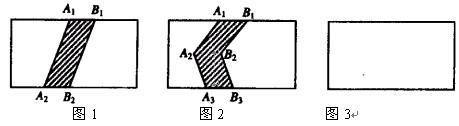
题目内容
现将连续自然数1至2009按图中的方式排列成一个长方形队列，再用正方形任意框出16个数。
（1）设任意一个这样的正方形框中的最小数为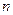
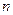，请用的代数式表示该框中的16个数，然后填入右表中相应的空格处，并求出这16个数中的最小数和最大数，然后填入右表中相应的空格处，并求出这16个数的和。（用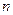的代数式表示）
（2）在图中，要使一个正方形框出的16个数之和和分别等于832、2000、2008是否可能？若不可能，请说明理由；若可能，请求出该正方形框出的16个数中的最小数和最大数
| | | | |
| | | | |
| | | | |
| | | | |
|
（1）设任意一个这样的正方形框中的最小数为
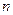，请用的代数式表示该框中的16个数，然后填入右表中相应的空格处，并求出这16个数中的最小数和最大数，然后填入右表中相应的空格处，并求出这16个数的和。（用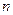的代数式表示）（2）在图中，要使一个正方形框出的16个数之和和分别等于832、2000、2008是否可能？若不可能，请说明理由；若可能，请求出该正方形框出的16个数中的最小数和最大数
（1）略
（2）不存在，理由略
（1）
n n+1 n+2 n+3
n+7 n+8 n+9 n+10
n+14 n+15 n+16 n+17
n+21 n+22 n+23 n+24
这16个的和=16n+192=16（n+12）
（2）设16（n+12）="832 " n="40 "
∴存在最小为40，最大40+24=64
16（n+12）="2000 " n="113 "
∴存在最小为113，最大为137，
16（n+2）="2008 " n=125.5，
∴不存在
n n+1 n+2 n+3
n+7 n+8 n+9 n+10
n+14 n+15 n+16 n+17
n+21 n+22 n+23 n+24
这16个的和=16n+192=16（n+12）
（2）设16（n+12）="832 " n="40 "
∴存在最小为40，最大40+24=64
16（n+12）="2000 " n="113 "
∴存在最小为113，最大为137，
16（n+2）="2008 " n=125.5，
∴不存在
练习册系列答案
阅读快车系列答案
相关题目
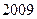年
月开始执行，深圳市红色的士调价前后的收费标准对比如下:调整前,起步价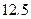
元/
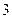公里，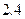
元/公里，无返空费；调整后,起步价
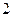公里，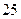
公里的，超出部分按里程价的
加收返空费．（不考虑红灯等因素）
公里换车”规避返空费的方法：即乘客的行程超过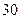
、
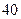公里换与不换的方法： 
元；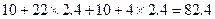
元，因此，行程
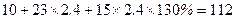元，若换车，总费用为：
元，则可节约
元．所以，行程为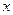
公里（
），不换车的费用
（元），换车的费用
（元），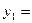
；
．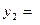