题目内容
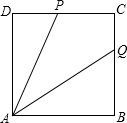 (1)如图,已知:P是正方形ABCD的CD边上一点,∠BAP的平分线交BC于Q,求证:AP=DP+BQ.
(1)如图,已知:P是正方形ABCD的CD边上一点,∠BAP的平分线交BC于Q,求证:AP=DP+BQ.
(2)若(1)中的点P位置在DC的延长线上,其他条件不变,结论是否仍然成立?请简单说明理由.
 解:(1)把△ABQ绕点A逆时针旋转90°到△ADE的位置,
解:(1)把△ABQ绕点A逆时针旋转90°到△ADE的位置,∴∠EAD=∠QAB,∠EDA=∠ABQ=90°,∠E=∠AQB,DE=BQ,
∴AB与AD重合,∠ADE=∠B=90°
∵AB=AD,
∴B、D两点重合,
∴点E,D,P共线,
又∵∠AQB=∠DAQ,
而∠BAP的平分线交BC于Q,
∴∠AQB=∠EAP,
∴∠E=∠PAE,
∴PE=PA,
∴PA=DP+BQ;

(2)PA=DP+BQ仍然成立.理由如下:
把△ABQ绕点A逆时针旋转90°到△ADE的位置,如图,
证明的方法和上面一样.
分析:(1)把△ABQ绕点A逆时针旋转90°到△ADE的位置,根据旋转的性质得∠EAD=∠QAB,∠EDA=∠ABQ=90°,∠E=∠AQB,DE=BQ,得到点E,D,P公线,而∠AQB=∠DAQ,∠BAP的平分线交BC于Q,所以∠AQB=∠EAP,则∠E=∠PAE,得到PE=PA,即可得到PA=DP+BQ;
(2)PA=DP+BQ仍然成立.把△ABQ绕点A逆时针旋转90°到△ADE的位置,证明的方法和上面一样.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.同时考查了正方形的性质和等腰三角形的性质.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
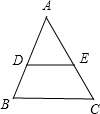 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
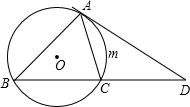 =2,∠ADC=30°
=2,∠ADC=30°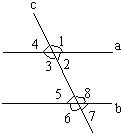 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=