题目内容
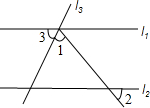 如图,直线l1∥l2,且l1,l2被直线l3所截,若∠1=70°,∠2=56°,则∠3等于( )
如图,直线l1∥l2,且l1,l2被直线l3所截,若∠1=70°,∠2=56°,则∠3等于( )分析:根据“两直线平行,同旁内角互补”得到∠1+∠2+∠4=180°,再利用对顶角相等得∠4=∠2=56°,而∠1=70°,然后代入计算即可.
解答:解:如图,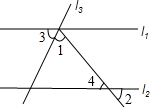
∵l1∥l2,
∴∠1+∠2+∠4=180°,
又∵∠4=∠2=56°,∠1=70°,
∴70°+56°+∠3=180°,
∴∠3=54°.
故选B.

∵l1∥l2,
∴∠1+∠2+∠4=180°,
又∵∠4=∠2=56°,∠1=70°,
∴70°+56°+∠3=180°,
∴∠3=54°.
故选B.
点评:本题考查了平行线的性质:两直线平行,同旁内角互补.也考查了对顶角相等.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
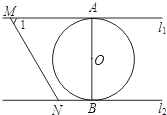 如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )
如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( )A、MN=
| ||||
B、若MN与⊙O相切,则AM=
| ||||
| C、若∠MON=90°,则MN与⊙O相切 | ||||
| D、l1和l2的距离为2 |
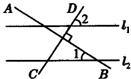 23、如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是
23、如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是 如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是
如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是 14、如图,直线l1∥l2,∠1=55°,∠2=65°,则∠3=
14、如图,直线l1∥l2,∠1=55°,∠2=65°,则∠3= (2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是
(2009•无锡二模)如图,直线L1∥L2,AB⊥CD,∠1=34°,那么∠2的度数是