题目内容
【题目】如图,在平面直角坐标系中,直线 y 2x 4 与 x 轴、 y 轴分别交于 A 、 B 两点.
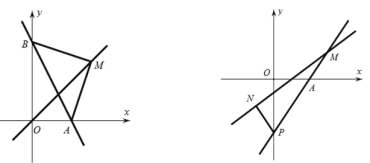
(1)求 A 、 B 两点的坐标;
(2)若点 M 为直线 y mx 上一点,且ABM 是等腰直角三角形,求 m 的值;
(3)过 A 点的直线 y kx 2k 交 y 轴负半轴于 P ,N 点的横坐标为1,过 N 点的直线![]() 于点 M ,试探究 PM 与 PN 之间的数量关系.
于点 M ,试探究 PM 与 PN 之间的数量关系.
【答案】(1)![]() ;(2)当m>0时,m的值为1或
;(2)当m>0时,m的值为1或![]() 或
或![]() ;当m<0时,m的值为:-
;当m<0时,m的值为:-![]() 或-2;(3)
或-2;(3)![]()
【解析】
(1)根据直线 y 2x 4 与 x 轴、 y 轴分别交于 A 、 B 两点,分别令y=0 ,x=0,求出即可;
(2)当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,证△BMN≌△ABO(AAS),求出M的值即可;②当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,同法求出M的值;③当AM⊥BM,且AM=BM时,过M作MN⊥x轴于N,MH⊥y轴于H,证△BHM≌△AMN,求出M的值即可.
(3)设NM与x轴的交点为H,分别过M、H作x轴的垂线垂足为G,HD交MP于D点,求出H、G的坐标,证△AMG≌△ADH,△AMG≌△ADH≌△DPC≌△NPC,推出PN=PD=AD=AM代入即可求出答案.
解:(1)y 2x 4 与 x 轴、 y 轴分别交于 A 、 B 两点
令y=0,则x=2; 令x=0,则y=4![]()
![]()
(2) (i)当m>0时,分三种情况:
①如图1,
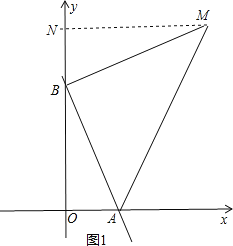
当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,
∵BM⊥BA,MN⊥y轴,OB⊥OA,
∴∠MBA=∠MNB=∠BOA=90°,
∴∠NBM+∠NMB=90°,∠ABO+∠NBM=90°,
∴∠ABO=∠NMB,
在△BMN和△ABO中,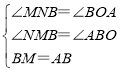 ,
,
∴△BMN≌△ABO(AAS),
MN=OB=4,BN=OA=2,
∴ON=2+4=6,
∴M的坐标为(4,6),
代入y=mx得:m=![]() ,
,
②如图2,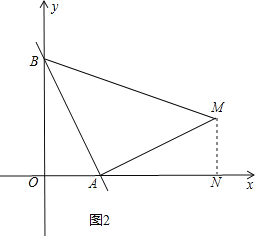
当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,△BOA≌△ANM(AAS),同理求出M的坐标为(6,2),m=![]() ,
,
③如图4,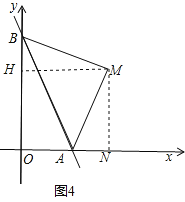
当AM⊥BM,且AM=BM时,过M作MN⊥X轴于N,MH⊥Y轴于H,则△BHM≌△AMN,
∴MN=MH,
设M(x,x)代入y=mx得:x=mx,
∴m=1,
答:m的值是![]() 或
或![]() 或1;
或1;
(ii)当m<0时,由(i)得:关于直线AB:y=-2x+4,
同理可得:m=-![]() 或-2;
或-2;
(3)解:如图,
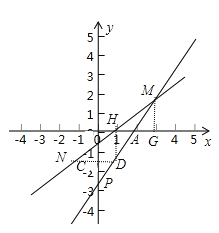
设NM与x轴的交点为H,过M作![]() 轴于G,过H作
轴于G,过H作![]() 轴,HD交MP于D点,连接ND,
轴,HD交MP于D点,连接ND,
由![]() 与x轴交于H点,
与x轴交于H点,![]() ,
,
由![]() 与
与![]() 交于M点,
交于M点,![]() ,
,
而![]() ,
,![]() 为HG的中点,
为HG的中点,![]() ,
,
又![]() N点的横坐标为-1,且在
N点的横坐标为-1,且在![]() 上,可得N 的纵坐标为-k,同理P的纵坐标为
上,可得N 的纵坐标为-k,同理P的纵坐标为![]() ,
,![]() 平行于x轴,且N、D的横坐标分别为-1、1
平行于x轴,且N、D的横坐标分别为-1、1![]() 与D关于y轴对称,
与D关于y轴对称,![]() ,
,![]() ,
,![]()
![]()
![]()

 同步练习强化拓展系列答案
同步练习强化拓展系列答案