题目内容
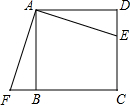 如图,四边形ABCD是正方形,点E是边CD上一点,点F是CB延长线上一点,且DE=BF=4,解答下列问题:
如图,四边形ABCD是正方形,点E是边CD上一点,点F是CB延长线上一点,且DE=BF=4,解答下列问题:(1)求证:△ABF≌△ADE;
(2)指出△AFB是由△AED怎样旋转得到的?并求出旋转过程中线段DE所扫过的区域的面积(列式计算即可).
考点:旋转的性质,全等三角形的判定与性质,正方形的性质,扇形面积的计算
专题:
分析:(1)根据SAS即可证明△ABF≌△ADE;
(2)△AFB是由△AED绕点A旋转90°得到的,再根据线段DE扫过的面积等于以AE、D为半径的两个扇形的面积的差列式计算即可得解.
(2)△AFB是由△AED绕点A旋转90°得到的,再根据线段DE扫过的面积等于以AE、D为半径的两个扇形的面积的差列式计算即可得解.
解答:(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠ADE=∠ABF=90°,
在△ABF和△ADE中,
,
∴△ABF≌△ADE;
(2)△AFB是由△AED绕点A旋转90°得到的,
理由如下:
∵△ABF≌△ADE,
∴AD=AB,
即AD和AB是对应边,
∵∠BAD=90°,
∴△AFB是由△AED绕点A旋转90°得到的,
由题意可知:据线段DE扫过的面积等于以AE、D为半径的两个扇形的面积=
-
=
π(AE2-AD2),
∵DE=BF=4,
∴由勾股定理得:AE2-AD2=DE2=16,
∴线段DE所扫过的区域的面积=
π×16=4π.
∴AD=AB,∠ADE=∠ABF=90°,
在△ABF和△ADE中,
|

∴△ABF≌△ADE;
(2)△AFB是由△AED绕点A旋转90°得到的,
理由如下:
∵△ABF≌△ADE,
∴AD=AB,
即AD和AB是对应边,
∵∠BAD=90°,
∴△AFB是由△AED绕点A旋转90°得到的,
由题意可知:据线段DE扫过的面积等于以AE、D为半径的两个扇形的面积=
| 90π•AE2 |
| 360 |
| 90π•AD2 |
| 360 |
| 1 |
| 4 |
∵DE=BF=4,
∴由勾股定理得:AE2-AD2=DE2=16,
∴线段DE所扫过的区域的面积=
| 1 |
| 4 |
点评:本题考查了利用旋转变换作图,正方形的性质,全等三角形的判定和性质以及勾股定理的应用,扇形面积的计算,其中(2)问理解线段DE扫过的面积的表示方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
要使分式
的值为0,则x应该等于( )
| x2+5x+4 |
| x+4 |
| A、-4或-1 | B、-4 |
| C、-1 | D、4或1 |
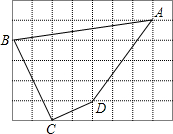 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1.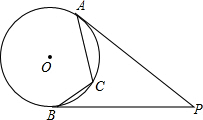 如图,已知PA、PB是⊙O的两条切线,切点分别为A、B,点C是劣弧AB上的任意一点,∠P=40°,则∠ACB=
如图,已知PA、PB是⊙O的两条切线,切点分别为A、B,点C是劣弧AB上的任意一点,∠P=40°,则∠ACB=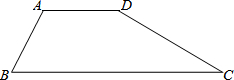 如图,水坝的横断面为梯形ABCD,迎水坡AB的坡度为
如图,水坝的横断面为梯形ABCD,迎水坡AB的坡度为