题目内容
(2007•江西模拟)如图,在△ABC中,已知:AC=3,BC=4,AB=5,以AC为直径作⊙O交AB于点D.(1)求证:BC是⊙O的切线;
(2)连CD,求tan∠ACD的值.
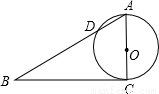
【答案】分析:(1)即证BC⊥AC.根据三边长易证△ABC是直角三角形,得证;
(2)连接CD,则CD⊥AB.证明∠ACD=∠B,运用三角函数求解.
解答:证明:(1)∵AC=3,BC=4,AB=5,
∴AC2+BC2=32+42=25=AB2,
∴∠ACB=90°即OC⊥BC.
又点C在⊙O上,
∴BC是⊙O的切线.

(2)连CD.
∵AC是直径,
∴∠ADC=90°.
∴∠ACD+∠A=90°.
又∠B+∠A=90°,
∴∠ACD=∠B.
则tan∠ACD=tan∠B=AC:BC=3:4.
点评:此题考查了直角三角形的判定、切线的判定、三角函数的定义等知识点,难度中等.
(2)连接CD,则CD⊥AB.证明∠ACD=∠B,运用三角函数求解.
解答:证明:(1)∵AC=3,BC=4,AB=5,
∴AC2+BC2=32+42=25=AB2,
∴∠ACB=90°即OC⊥BC.
又点C在⊙O上,
∴BC是⊙O的切线.

(2)连CD.
∵AC是直径,
∴∠ADC=90°.
∴∠ACD+∠A=90°.
又∠B+∠A=90°,
∴∠ACD=∠B.
则tan∠ACD=tan∠B=AC:BC=3:4.
点评:此题考查了直角三角形的判定、切线的判定、三角函数的定义等知识点,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(2007•江西模拟)下表是我国近几年的进口额与出口额数据(近似值)统计表:
(1)下图是描述这两组数据的折线图,请你将出口额、进口额的折线图补充完整;

(2)计算并比较1998年至2000年及2000年至2002年出口额年平均增长率(结果保留三个有效数字);
(3)观察折线图,你还能得到什么信息,写出两条(根据信息的价值评分).
| 年份 | 1985 | 1990 | 1995 | 1998 | 2000 | 2002 | 2005 |
| 出口额(亿美元) | 274 | 621 | 1500 | 1800 | 2500 | 3256 | 7620 |
| 进口额(亿美元) | 423 | 534 | 1300 | 1400 | 2300 | 2952 | 6601 |

(2)计算并比较1998年至2000年及2000年至2002年出口额年平均增长率(结果保留三个有效数字);
(3)观察折线图,你还能得到什么信息,写出两条(根据信息的价值评分).
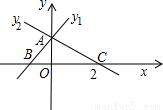
 +x-1的图象,绕原点旋转180°,所得图象的函数表达式是______;
+x-1的图象,绕原点旋转180°,所得图象的函数表达式是______;