题目内容
【题目】如图:在正方形ABCD中,点P、Q是CD边上的两点,且DP=CQ,过D作DG⊥AP于H,交AC、BC分别于E,G,AP、EQ的延长线相交于R.
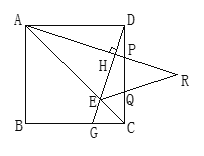
(1)求证:DP=CG;
(2)判断△PQR的形状,请说明理由.
【答案】(1)证明见解析;(2)△PQR为等腰三角形,理由见解析.
【解析】
(1)正方形对角线AC是对角的角平分线,可以证明△ADP≌△DCG,即可求证DP=CG.
(2)由(1)的结论可以证明△CEQ≌△CEG,进而证明∠PQR=∠QPR.故△PQR为等腰三角形.
(1)证明:在正方形ABCD中,
AD=CD,∠ADP=∠DCG=90°,
∠CDG+∠ADH=90°,
∵DH⊥AP,∴∠DAH+∠ADH=90°,
∴∠CDG=∠DAH,
∴△ADP≌△DCG,
∵DP,CG为全等三角形的对应边,
∴DP=CG.
(2)△PQR为等腰三角形.
∵∠QPR=∠DPA,∠PQR=∠CQE,CQ=DP,由(1)的结论可知
∴CQ=CG,∵∠QCE=∠GCE,CE=CE,
∴△CEQ≌△CEG,即∠CQE=∠CGE,
∴∠PQR=∠CGE,
∵∠QPR=∠DPA,
∴∠PQR=∠QPR,
所以△PQR为等腰三角形.

练习册系列答案
相关题目