题目内容
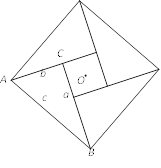
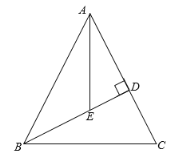
【题目】如图,在等腰△ABC中,AB=AC=10,高BD=8,AE平分∠BAC,则△ABE的面积为________.
【答案】15.
【解析】
延长AE交BC于点F,过E点作GE![]() AB.在Rt△ADB中,根据勾股定理得到AD,进一步得到CD;在Rt△BDC中,根据勾股定理得到BC;根据等腰三角形的性质和角平分线的性质得到CF,在Rt△AFC中,根据勾股定理得到AF,通过AA证明△DAE∽△FAC,根据相似三角形的性质求解CE,根据角平分线的性质可得GE=DE,然后即可求解△ABE的面积.
AB.在Rt△ADB中,根据勾股定理得到AD,进一步得到CD;在Rt△BDC中,根据勾股定理得到BC;根据等腰三角形的性质和角平分线的性质得到CF,在Rt△AFC中,根据勾股定理得到AF,通过AA证明△DAE∽△FAC,根据相似三角形的性质求解CE,根据角平分线的性质可得GE=DE,然后即可求解△ABE的面积.
解:延长AE交BC于点F,过E点作GE![]() AB
AB
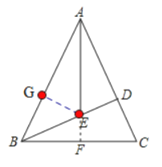
∵在△ABC中,AB=AC=3,高BD=8,
∴在Rt△ADB中,AD=![]() =6,
=6,
∴CD=AC-AD=4,
∴在Rt△BDC中,BC=![]() ,
,
∵AE平分∠BAC,
∴EG=DE,CF=![]() BC=
BC=![]() ,∠AFC=90°,
,∠AFC=90°,
∴在Rt△AFC中,AF=![]() =
=![]() ,
,
∵∠DAE=∠FAC,∠ADE=∠AFC=90°,
∴△DAE∽△FAC,
∴DE:AD=CF:AF,
![]()
∴EG=DE=3
∴SABE=![]()
故答案为:15.

练习册系列答案
相关题目