题目内容
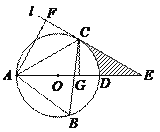
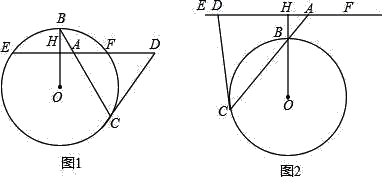
【题目】如图1,A为⊙O的弦EF上的一点,OB是和这条弦垂直的半径,垂足为H,BA的延长线交⊙O于点C,过点C作⊙O的切线与EF的延长线相交于点D.
(1)求证:DA=DC;
(2)当DF:EF=1:8,且DF=![]() 时,求ABAC的值;
时,求ABAC的值;
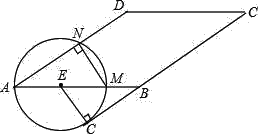
(3)将图1中的EF所在直线往上平行移动到⊙O外,如图2的位置,使EF与OB,延长线垂直,垂足为H,A为EF上异于H的一点,且AH小于⊙O的半径,AB的延长线交⊙O于C,过C作⊙O的切线交EF于D.试猜想DA=DC是否仍然成立?并证明你的结论.
【答案】(1)见解析;(2)24;(3)见解析.
【解析】
(1)连接过切点的半径OC,根据等角的余角相等进行证明∠ACD=∠DAC,从而得到AD=CD;
(2)根据已知条件求得DF的长,再根据切割线定理求得CD的长.从而求得DF和EF的长,最后根据相交弦定理即可求得它们的乘积;
(3)作直径,构造了直角三角形,也构造了弦切角所夹的弧所对的圆周角.根据等角的余角相等证明∠DAC=∠ACD,从而证明结论.
(1)连接OC,则OC⊥DC,
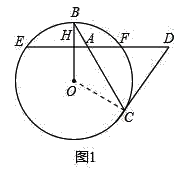
∴∠DCA=90°﹣∠ACO=90°﹣∠B,
∵∠DAC=∠BAE=90°﹣∠B,
∴∠DAC=∠DCA,
∴DA=DC;
(2)∵DF:EF=1:8,
∵DF=![]() ,
,
∴EF=8DF=8![]() ,
,
∵DC为⊙O的切线,
∴DC2=DFDE=![]() ×9
×9![]() =18,
=18,
∵DC=3![]() ,
,
∴AF=2![]() ,AE=6
,AE=6![]() ,
,
∴ABAC=AEAF=24;
(3)结论DA=DC仍然成立.
理由如下:延长BO交⊙O于K,连接CK,则∠KCB=90°,
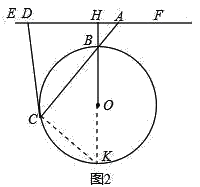
∵DC为⊙O的切线,
∴∠DCA=∠CKB=90°﹣∠CBK,
∵∠CBK=∠HBA,
∴∠BAH=90°﹣∠HBA=90°﹣∠CBK,
∴∠DCA=∠BAH,
∴DA=DC.

练习册系列答案
相关题目