Question

如图，等腰梯形ABCD中，AD∥BC，AB=DC，对角线AC和BD交于点O，BC=8cm，BD=6cm，梯形的高为3cm．E是BC边上的一个动点（点E不与B、C两点重合），EF∥BD交AC于点F，EG∥AC交BD于点G．
（1）如图①，在点E运动过程中，试猜测GE、EF的长度和有什么特点？说明你的理由．
（2）如图②，在点E运动过程中，若点E到BD、AC的垂线段分别为EP、EQ，你能确定EP+EQ的值吗？

Answer 1

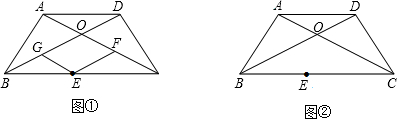
解：（1）GE、EF的长度和的特点是GE+EF=OB．
理由是：∵等腰梯形ABCD，AD∥BC，AB=DC，
∴∠ABC=∠DCB，
∵BC=BC，AB=DC，
∴△ABC≌△DCB，
∴∠OBC=∠OCB，
∴OB=OC，
∵EG∥AC，
∴∠GEB=∠OCB，
∴∠GEB=∠OBC，
∴BG=GE，
∵EG∥AC，EF∥BD，
∴四边形OGEF是平行四边形，
∴EF=OG，
∴EG+EF=BG+OG=OB，
即GE+EF=OB．

（2）EP+EQ=4，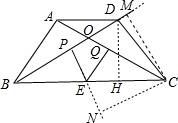
理由是：
过D作DH⊥BC于H，过C作CM⊥BD交BD的延长线与M，CN⊥PE于N，
在△BDC中由三角形的面积公式得：BC•DH=BD•CM，
BC×DH=BD×CM，
8×3=6CM，
∴CM=4，
∵CM⊥BD，CN⊥PE，EP⊥BD，
∴∠N=∠CMP=∠EPM=90°，
∴四边形NPMC是矩形，
∴PN=CM=4，CN∥BD，
∴∠OBC=∠BCN，
∵∠OBC=∠OCB，
∴∠OCB=∠BCN，
∵EQ⊥AC，
∴∠EQC=∠N=90°，
∴QE=EN，
∴EP+EQ=EN+EP=PN=4，
即EP+EQ=4．
分析：（1）根据等腰梯形的性质求出∠ABC=∠DCB，证△ABC≌△DCB，推出∠OBC=∠OCB，证GB=GE即可推出答案；
（2）过D作DH⊥BC于H，过C作CM⊥BD交BD的延长线与M，CN⊥PE于N，求出△BDC的高CM，证矩形NPMC，推出CM=PN=4，证∠OCB=∠BCN，推出EN=EQ，求出PN=PE+EQ即可．
点评：本题主要考查对等腰梯形的性质，等腰三角形的性质和判定，平行线的性质，平行四边形的性质和判定，矩形的性质和判定，三角形的面积，角平分线的性质，垂线等知识点的理解和掌握，综合运用这些性质进行推理是解此题的关键．