题目内容
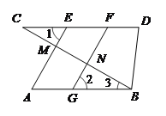
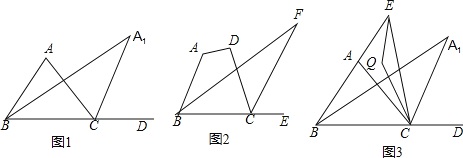
【题目】如图，在四边形ABCD中，
，
，
，
，点E在AB边上，
，
．
求CE的长度；
求证：
≌
；
设点P是线段AB上的一个动点，求
的最小值是多少？
【答案】（1）5，（2）见解析，（3） 
的最小值为
．
【解析】
由
，
，
，根据勾股定理求出CE；
先证出
，即可证明
≌
；
作点D关于AB的对称点F，连接CF交AB于点P，再用勾股定理求出CF的长即为的最小值．
解：
，，，
根据勾股定理可得：
；
，
，
，
，
，
，，
，
在和中，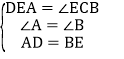
≌
；
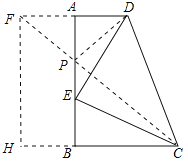
延长DA至F，使得
，并连接CF，此时CF与AB的交点为点P，连接PD；
，且，
是等腰三角形，
，
的最小值为CF，
过点F作FH垂直CB的长线，垂足为H，如图所示：
根据题意得：
，
，
根据勾股定理可得，
，
即的最小值为．
故答案为：（1）5，（2）见解析，（3） 的最小值为．
练习册系列答案
相关题目
【题目】某校举行了“文明在我身边”摄影比赛．已知每幅参赛作品成绩记为x分(60≤x＜100)．校方从600幅参赛作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制了如下不完整的统计图表．
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |
根据以上信息解答下列问题：
(1)统计表中c的值为________；样本成绩的中位数落在分数段________中；
(2)补全频数直方图；
(3)若80分以上(含80分)的作品将被组织展评，试估计全校被展评的作品数量是多少．
