题目内容
【题目】在![]() 中,
中,![]() ,
,
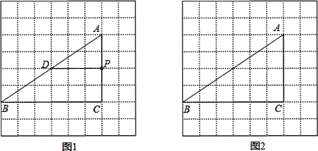
(1)如图![]() ,
,![]() 是
是![]() 上的点,过点
上的点,过点![]() 作直线截
作直线截![]() ,使截得的三角形与
,使截得的三角形与![]() 相似.例如:过点
相似.例如:过点![]() 作
作![]() 交
交![]() 于
于![]() ,则截得的
,则截得的![]() 与
与![]() 相似.请你在图中画出所有满足条件的直线.
相似.请你在图中画出所有满足条件的直线.
(2)如图![]() ,
,![]() 是
是![]() 上异于点
上异于点![]() ,
,![]() 的动点,过点
的动点,过点![]() 作直线截
作直线截![]() ,使截得的三角形与
,使截得的三角形与![]() 相似,直接写出满足条件的直线的条数.(不要求画出具体的直线)
相似,直接写出满足条件的直线的条数.(不要求画出具体的直线)
【答案】见解析
【解析】
(1)利用平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似的判定定理过点P作两条,再利用两组对应角相等的两个三角形相似的判定定理,过点P作两条.
(2)把Q点看成从C点出发到B点的动点,发现当Q点在某一个位置时,所作截的三角形与原三角形相似的数量减少了一个,通过此时的临界条件把QC的长度计算出来,进行分类说明.
(1)如图所示:
第一种:利用平行于三角形一边的直线和其他两边相交,所截得的三角形与原三角形相似的判定定理,过点P分别做AB与BC的平行线PD与PE.分别得到△ADP∽△ABC. △PCE∽△ACB.
第二种:利用两组对应角相等的两个三角形相似的判定定理,过P分别做PG垂直AB于点G,做PF交BC于点F,使∠PFC=∠A.分别得到△AGP∽△ACB, △FPC∽△ACB.
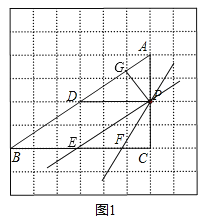
(2)
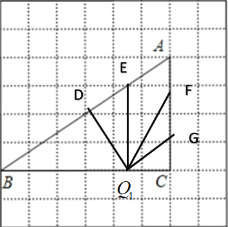
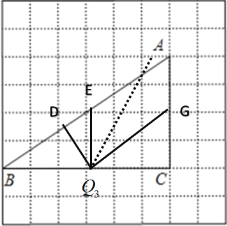
如图所示,假设点Q从点C开始往点B移动,由(1)可知,作QD⊥AB,
得△BQD∽△BAC.作QF交AC于点F,使∠QFC=∠B,得△QCF∽△ACB.
作QE∥AC,得△BQE∽△BCA.作QG∥AB,得△QCG∽△BCA.
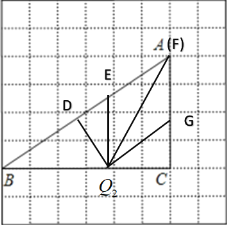
当移动到![]() 位置时,此时出现点F于点A重合,此时是一个临界点,利用△QCF∽△ACB得到
位置时,此时出现点F于点A重合,此时是一个临界点,利用△QCF∽△ACB得到![]() ,则
,则![]() 又此时CA=CF,所以QC=
又此时CA=CF,所以QC=![]()
该点往左移动,不能在三角形ABC内做出作QF交AC于点F,该点往右移动,可以在三角形ABC内做出作QF交AC于点F,使△QCF∽△ACB.
故当0<QC≤![]() 时,满足条件的直线有4条;
时,满足条件的直线有4条;
当![]() <QC<6时,满足条件的直线有3条.
<QC<6时,满足条件的直线有3条.