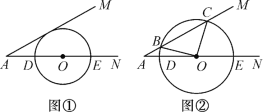题目内容
【题目】已知:△ABC是⊙O的内接三角形,且AB=BC,点D为劣弧BC上的一点,连接BD、DC.
(1)如图1,若∠BDC=120°,求证:△ABC是等边三角形;
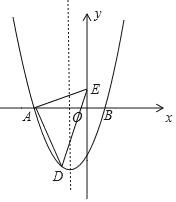
(2)如图2,在(1)的条件下,线段CD绕点C顺时针旋转60°,得到线段CE,连接AE,求证:BD=AE;
(3)如图3,在(2)的条件下,连接OE,若⊙O的半径为![]() ,OE=2,求BD的长.
,OE=2,求BD的长.
【答案】(1)见解析;(2)见解析;(3)BD=3![]() .
.
【解析】
(1)根据圆内接四边形的性质和等边三角形的判定解答即可;
(2)根据等边三角形的性质和全等三角形的判定证明即可;
(3)连接ED,利用勾股定理和直角三角形的性质解答即可.
证明:(1)∵四边形ABDC内接于⊙O,
∴∠BDC+∠BAC=180°,
∴∠BAC=180°-∠BOA=180°-120°=60°.
∵BA=BC,
∴△ABC是等边三角形.
(2)由(1)知△ABC是等边三角形,
∴∠BCA=60°,
∵∠DCE=60°,
∴∠BCA=∠DCE
而∠BCA=∠BCE+∠ECA,∠DCE=∠BCD+∠BCE,
∴∠ECA=∠DCB,
∵在△CDB与△CEA中
 ,
,
∴△CDB≌△CEA(SAS)
∴DB=AE;
(3)连接ED,可知△CDE为等边三角形,
∴∠DCE=∠DEC=∠EDC=60°,
∵∠BDC=120°
由(2)知△CDB≌△CEA,
∴∠BDC=∠AEC=120°,∠DEC+∠AEC=180°,
∴A、E、D三点在同一直线上,连接OD、OC,
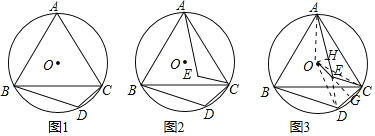 ,
,
∵OD=OC,ED=EC,
∴OE是线段DC的中垂线,
∴OE是∠DEC平分线,
设直线OE与CD的交点为G,则有∠EDG=![]() ∠DEC=30°,
∠DEC=30°,
∴∠OEA=∠DEG=30°,
连接OA,过点O作OH⊥AE,垂足为H,
在直角三角形OEH中,OE=2,∠OEA=30°,
∴OH=![]() OE=1
OE=1
可得EH=![]() ,
,
在直角三角形OAH中,OA=![]() ,OH=1,根据勾股定理,得AH=2
,OH=1,根据勾股定理,得AH=2![]() ,
,
∴AE=AH+HE=3![]() ,
,
∴BD=AE=3![]() .
.

 新思维假期作业暑假吉林大学出版社系列答案
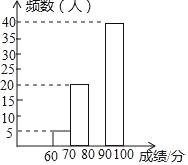
新思维假期作业暑假吉林大学出版社系列答案【题目】某校组织了一次全校2000名学生参加的比赛,赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了100名学生的成绩(成绩x取整数,满分100分)作为样本进行整理,得到下列不完整的统计表:
请依据所给信息,解答下列问题:
(1)直接填空:a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)请自己提出一个与该题信息相关的问题,并解答你提出的问题.
成绩x/分 | 频数 | 频率 |
60≤x<70 | 5 | 0.05 |
70≤x<80 | 20 | b |
80≤x<90 | a | c |
90≤x≤100 | 40 | 0.40 |