题目内容
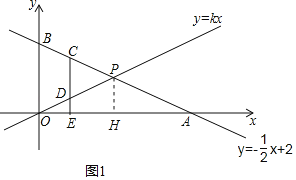
【题目】如图，在平面直角坐标系中，一次函数y＝﹣
x+2的图象交x轴、y轴分别于点A，B，交直线y＝kx于P．
（1）求点A、B的坐标；
（2）若OP＝PA，求P点坐标及k的值．
（3）在（2）的条件下，C是直线BP上一动点，CE⊥x轴于E，交直线DP于D，若CD＝3ED，直接写出C点的坐标．
【答案】（1）点A的坐标为（4，0），点B的坐标为（0，2）；（2）点P的坐标为（2，1），k＝
；（3）点C的坐标为（﹣4，4）或（
，
）．
【解析】
（1）分别代入x＝0、y＝0求出y、x的值，由此可得出点B、A的坐标；
（2）作PH⊥OA于H，根据等腰三角形的性质可得出点P的坐标，再由点P在直线y＝kx上求出k值；
（3）设点C的坐标为（m，﹣m+2），得到点D的坐标为（m，m），得出CD、DE的长度，由题意得出关于m的一元一次方程，解方程得出结论．
解：（1）对于一次函数y＝﹣x+2，
当y＝0时，x＝4，
当x＝0时，y＝2，
∴点A的坐标为（4，0），点B的坐标为（0，2）；
（2）如图1，作PH⊥OA于H，
∵OP＝AP，PH⊥OA，
∴OH＝OA＝OA＝2，
∴点P的横坐标为2，
∵点P在直线y＝﹣x+2上，
∴点P的纵坐标y＝﹣×2+2＝1，
∴点P的坐标为（2，1）．
∵点P在直线y＝kx上，
∴1＝2k，解得：k＝；
（3）设点C的坐标为（m，﹣m+2），则点D的坐标为（m，m），
∴CD＝|﹣m+2﹣m|＝|2﹣m|，DE＝|m|．
当m＜0时，2﹣m＝3×（﹣m），
解得，m＝﹣4，
则点C的坐标为（﹣4，4）；
当0＜m＜2时，2﹣m＝3×m，
解得，m＝，
则点C的坐标为（，）；
当2＜m＜4时，不存在点C；
当m＞4时，m﹣2＝3×m，
解得，m＝﹣4（不合题意），
综上所述，CD＝3ED时，点C的坐标为（﹣4，4）或（，）．
