题目内容
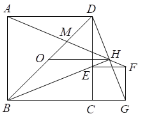
【题目】如图,四边形ABCD、CEFG都是正方形,E在CD上且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,下列四个结论:
① BE⊥GD; ② OH=![]() BG; ③ ∠AHD=45°; ④ GD=
BG; ③ ∠AHD=45°; ④ GD=![]() AM.
AM.
其中正确的结论个数有
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①由已知条件可证得△BEC≌△DGC,∠EBC=∠CDG,因为∠BDC+∠DBH+∠EBC=90°,所以∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;
②由①可以证明△BHD≌△BHG,就可以得到DH=GH,得出OH是△BGD的中位线,从而得出结论.
③若以BD为直径作圆,那么此圆必经过A、B、C、H、D五点,根据圆周角定理即可得到∠AHD=45°,所以②的结论也是正确的.
④此题要通过相似三角形来解;由②的五点共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45°,由此可判定△ABM∽△DBG,根据相似三角形的比例线段即可得到AM、DG的比例关系;
解:①正确,证明如下:
∵BC=DC,CE=CG,∠BCE=∠DCG=90°,
∴△BEC≌△DGC,
∴∠EBC=∠CDG,
∵∠BDC+∠DBH+∠EBC=90°,
∴∠BDC+∠DBH+∠CDG=90°,即BE⊥GD,故①正确;
②∵BE平分∠DBC,
∴∠DBH=∠GBH.
∵BE⊥GD,
∴∠BHD=∠BHG=90°.
在△BHD和△BHG中
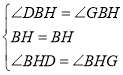 ,
,
∴△BHD≌△BHG(ASA),
∴DH=GH.
∵O是BD中点,
∴DO=BO.
∴OH是△BDG的中位线,
∴OH=![]() BG,故②正确;
BG,故②正确;
③由于∠BAD、∠BCD、∠BHD都是直角,因此A、B、C、D、H五点都在以BD为直径的圆上;
由圆周角定理知:∠DHA=∠ABD=45°,故③正确;
④由②知:A、B、C、D、H五点共圆,则∠BAH=∠BDH;
又∵∠ABD=∠DBG=45°,
∴△ABM∽△DBG,得AM:DG=AB:BD=1:![]() ,即DG=
,即DG=![]() AM;
AM;
故④正确;
∴正确的个数有4个.
故选:D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案