题目内容
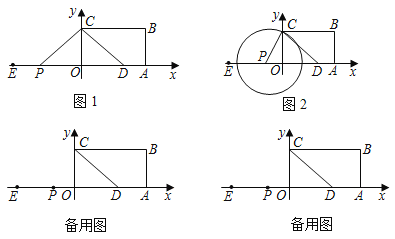
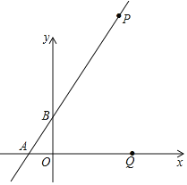
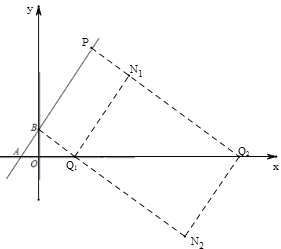
【题目】如图平面直角坐标系中,直线y=kx+1与x轴交于点A点,与y轴交于B点,P(a,b)是这条直线上一点,且a、b(a<b)是方程x2﹣6x+8=0的两根.Q是x轴上一动点,N是坐标平面内一点,以点P、B、Q、N四点为顶点的四边形恰好是矩形,则点N的坐标为_____或_____.
【答案】(![]() ,3) (6,﹣3)
,3) (6,﹣3)
【解析】
如图,作BQ1⊥AP,交x轴于Q1,PQ2⊥AP,交x轴于Q2,作Q1N1⊥PQ2于N1,Q2N2⊥BQ1,交BQ1延长线于N2,设Q1坐标为(m,0),求出方程x2﹣6x+8=0的两根可得P点坐标,代入y=kx+1可求出k值,进而可求出A点坐标,利用直角三角形两锐角互余的关系可得∠BQ1O=∠ABO,即可证明△BQ1O∽△ABO,△ABO根据相似三角形的性质即可求出m的值,可得Q1坐标,根据B、Q1坐标可得直线BQ1的解析式,根据PQ2//BQ1及P点坐标可得PQ2解析式,同理可求出Q1N1和Q2N2解析式,联立解析式即可求出N1和N2的坐标,即可得答案.
如图,作BQ1⊥AP,交x轴于Q1,PQ2⊥AP,交x轴于Q2,作Q1N1⊥PQ2于N1,Q2N2⊥BQ1,交BQ1延长线于N2,设Q1坐标为(m,0),
解方程x2﹣6x+8=0得x1=2,x2=4,
∵P(a,b)是这条直线上一点,且a、b(a<b)是方程x2﹣6x+8=0的两根,
∴点P坐标为(2,4),
∴4=2k+1,
解得k=![]() ,
,
∴AP的解析式为:y=![]() x+1,
x+1,
当y=0时,x=![]() ;当x=0时,y=1,
;当x=0时,y=1,
∴点A坐标为(![]() ,0),点B坐标为(0,1),
,0),点B坐标为(0,1),
∴OA=![]() ,OB=1,
,OB=1,
∵四边形BQ1N1P和四边形BN2Q2P是矩形,
∴∠ABQ1=90°,
∴∠ABO+∠OBQ1=90°,
∵∠BQ1O+∠OBQ1=90°,
∴∠BQ1O=∠ABO,
又∵∠AOB=∠BOQ1=90°,
∴△BQ1O∽△ABO,
∴![]() ,即
,即![]() ,
,
解得:m=![]() ,
,
∴Q1坐标为(![]() ,0),
,0),
设直线BQ1的解析式为y=x+b1,
∴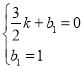 ,
,
解得: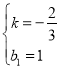 ,
,
∴直线BQ1的解析式为:y=![]() x+1,
x+1,
∵PQ2//BQ1,
∴设直线PQ2的解析式为:y=![]() x+b2,
x+b2,
∴![]() ×2+b2=4,
×2+b2=4,
解得:b2=![]() ,
,
∴直线PQ2的解析式为:y=![]() x+
x+![]() ,
,
当y=0时,x=8,
∴Q2坐标为(8,0),
∵Q1N1//Q2N2//AP,
∴同理可得:直线Q1N1的解析式为:y=![]() x-
x-![]() ,
,
直线Q2N2的解析式为:y=![]() x-12,
x-12,
联立Q1N1和PQ2解析式得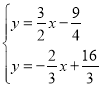 ,
,
解得:![]() ,
,
∴N1坐标为(![]() ,3)
,3)
联立Q2N2和BQ1解析式得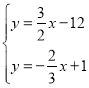 ,
,
解得:![]() ,
,
∴N2坐标为(6,-3),
综上所述:点N坐标为(![]() ,3)或(6,-3),
,3)或(6,-3),
故答案为:(![]() ,3),(6,-3),
,3),(6,-3),

 阅读快车系列答案
阅读快车系列答案