题目内容
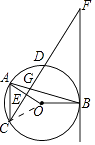
【题目】如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF. 
(1)求证:FG=FB.
(2)若tan∠F= ![]() ,⊙O的半径为4,求CD的长.
,⊙O的半径为4,求CD的长.
【答案】
(1)证明:∵OA=OB,
∴∠OAB=∠OBA,
∵OA⊥CD,
∴∠OAB+∠AGC=90°.
∵FB与⊙O相切,
∴∠FBO=90°,
∴∠FBG+OBA=90°,
∴AGC=∠FBG,
∵∠AGC=∠FGB,
∴∠FGB=∠FBG,
∴FG=FB
(2)解:如图,
设CD=a,
∵OA⊥CD,
∴CE= ![]() CD=
CD= ![]() a.
a.
∵AC∥BF,
∴∠ACF=∠F,
∵tan∠F= ![]()
tan∠ACF= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得AE= ![]() a,
a,
连接OC,OE=4﹣ ![]() a,
a,
∵CE2+OE2=OC2,
∴( ![]() a)2+(4﹣
a)2+(4﹣ ![]() a)2=4,
a)2=4,
解得a= ![]() ,
,
CD= ![]()
【解析】(1)根据等腰三角形的性质,可得∠OAB=∠OBA,根据切线的性质,可得∠FBG+OBA=90°,根据等式的性质,可得∠FGB=∠FBG,根据等腰三角形的判定,可得答案;(2)根据平行线的性质,可得∠ACF=∠F,根据等角的正切值相等,可得AE,根据勾股定理,可得答案.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案【题目】当前,“校园ipad现象已经受到社会的广泛关注,某教学兴趣小组对”“是否赞成中学生带手机进校园”的问题进行了社会调查.小文将调查数据作出如下不完整的整理: 频数分布表
看法 | 频数 | 频率 |
赞成 | 5 | |
无所谓 | 0.1 | |
反对 | 40 | 0.8 |

(1)请求出共调查了多少人;并把小文整理的图表补充完整;
(2)小丽要将调查数据绘制成扇形统计图,则扇形图中“赞成”的圆心角是多少度?
(3)若该校有3000名学生,请您估计该校持“反对”态度的学生人数.
【题目】某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图标信息回答下列问题: 体重频数分布表
组边 | 体重(千克) | 人数 |
A | 45≤x<50 | 12 |
B | 50≤x<55 | m |
C | 55≤x<60 | 80 |
D | 60≤x<65 | 40 |
E | 65≤x<70 | 16 |

(1)填空:①m=(直接写出结果); ②在扇形统计图中,C组所在扇形的圆心角的度数等于度;
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?



