题目内容
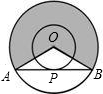如图，两同心圆的圆心为O，大圆的弦AB切小圆于P，两圆的半径分别为2和1，则弦长AB=分析：根据已知条件，连接OP，解直角三角形OPB即可得出PB的长，再利用垂径定理即可得出AB的长．
解答：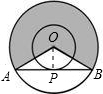
解：连接OP，
根据题意，可知OB=2．PO=1；
在Rt△OPB中，易得PB=
，
故AB=2
．
故答案为：2
．
解：连接OP，根据题意，可知OB=2．PO=1；
在Rt△OPB中，易得PB=
| 3 |
故AB=2
| 3 |
故答案为：2
| 3 |
点评：本题主要考查了切线的性质和垂径定理的应用以及解直角三角形等知识点，比较简单．
练习册系列答案
相关题目
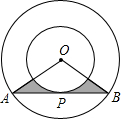如图，两同心圆的圆心为O，大圆的弦AB切小圆于P，两圆的半径分别为6，3，则图中阴影部分的面积是（ ）A、9
| ||
B、6
| ||
C、9
| ||
D、6
|
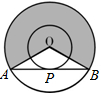如图，两同心圆的圆心为O，大圆的弦AB切小圆于P，两圆的半径分别为2和1，则弦长AB=
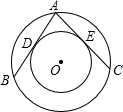如图，两同心圆的圆心为O，大圆的弦AB、AC分别切小圆于D、E两点，小圆的劣弧