题目内容
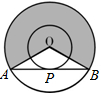 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,则弦长AB=
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,则弦长AB=分析:利用垂径定理根据勾股定理即可求得弦AB的长;利用相应的三角函数可求得∠AOB的度数,进而可求优弧AB的长度,除以2π即为圆锥的底面半径.
解答: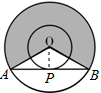 解:连接OP,则OP⊥AB,AB=2AP,
解:连接OP,则OP⊥AB,AB=2AP,
∴AB=2AP=2×
=2
,
∴sin∠AOP=
,
∴∠AOP=60°,
∴∠AOB=2∠AOP=120°,
∴优弧AB的长为
=
π,
∴圆锥的底面半径为
π÷2π=
.
 解:连接OP,则OP⊥AB,AB=2AP,
解:连接OP,则OP⊥AB,AB=2AP,∴AB=2AP=2×
| 22-12 |
| 3 |
∴sin∠AOP=
| ||
| 2 |
∴∠AOP=60°,
∴∠AOB=2∠AOP=120°,
∴优弧AB的长为
| 240π×2 |
| 180 |
| 8 |
| 3 |
∴圆锥的底面半径为
| 8 |
| 3 |
| 4 |
| 3 |
点评:本题综合考查了垂径定理,勾股定理,相应的三角函数,圆锥的弧长等于底面周长等知识点.

练习册系列答案
相关题目
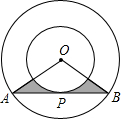 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是( )
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是( )A、9
| ||
B、6
| ||
C、9
| ||
D、6
|
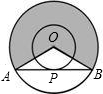 如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,则弦长AB=
如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为2和1,则弦长AB=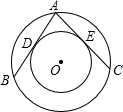 如图,两同心圆的圆心为O,大圆的弦AB、AC分别切小圆于D、E两点,小圆的劣弧
如图,两同心圆的圆心为O,大圆的弦AB、AC分别切小圆于D、E两点,小圆的劣弧