题目内容
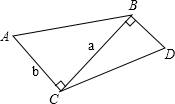如图，已知∠ACB=∠CBD=90°，AC=b，CB=a，当BD与a，b之间满足怎样的关系时，△ACB∽△CBD？
分析：根据如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；可知当满足AC：BC=BC：BD时，两三角形相似，因此只需将a、b代入比例关系式中进行求解即可．
解答：解：∵∠ACB=∠CBD=90°，
∴当
=
时，即当
=
时，△ACB∽△CBD，
∴BD=
．
因此当BD=
时，△ACB∽△CBD．
∴当
| AC |
| BC |
| BC |
| BD |
| b |
| a |
| a |
| BD |
∴BD=
| a2 |
| b |
因此当BD=
| a2 |
| b |
点评：本题主要考查相似三角形的判定，方法有：
①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；
②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；
③如果两个三角形的两个对应角相等，那么这两个三角形相似；
④平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似．
①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；
②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；
③如果两个三角形的两个对应角相等，那么这两个三角形相似；
④平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知∠ACB=∠CBD=90°，BC=a，AC=b，当CD=（ ）时，△CDB∽△ABC．A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，已知∠ACB=∠BDA=90°，要使△ABC≌△BAD，还需要添加一个条件，这个条件可以是
如图，已知∠ACB=90°，∠DAB=70°，AC平分∠DAB，∠1=35°．