题目内容
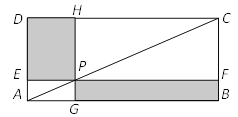
【题目】如图所示,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和点G,H.
(1)求证:△PHC≌△CFP;
(2)证明四边形 PEDH和四边形 PGBF都是矩形,并直接写出它们面积之间的关系。
【答案】(1)证明见解析;(2)证明见解析,面积相等.
【解析】试题分析:(1)由矩形的性质得出对边平行,再根据平行线的性质得出相等的角,结合全等三角形的判定定理AAS即可得出△PHC≌△CFP;
(2)由矩形的性质找出∠D=∠B=90°,再结合对边互相平行即可证出四边形PEDH和四边形PFBG都是矩形,通过角的正切值,在直角三角形中表示出直角边的关系,利用矩形的面积公式即可得出两矩形面积相等.
试题解析:(1)∵四边形ABCD为矩形,∴AB∥CD,AD∥BC.
∵PF∥AB,∴PF∥CD,∴∠CPF=∠PCH.
∵PH∥AD,∴PH∥BC,∴∠PCF=∠CPH.
在△PHC和△CFP中,∵∠CPF=∠PCH,PC=CP,∠PCF=∠CPH,∴△PHC≌△CFP(ASA).
(2)∵四边形ABCD为矩形,∴∠D=∠B=90°.
又∵EF∥AB∥CD,GH∥AD∥BC,∴四边形PEDH和四边形PFBG都是矩形.
∵EF∥AB,∴∠CPF=∠CAB.
在Rt△AGP中,∠AGP=90°,PG=AGtan∠CAB.
在Rt△CFP中,∠CFP=90°,CF=PFtan∠CPF.
S矩形DEPH=DEEP=CFEP=PFEPtan∠CPF;
S矩形PGBF=PGPF=AGPFtan∠CAB=EPPFtan∠CAB.
∵tan∠CPF=tan∠CAB,∴S矩形DEPH=S矩形PGBF.

练习册系列答案
相关题目