Question

如图1，已知抛物线C₁：y=a（x-1）²+4与直线C₂：y=x+b相交于点A（3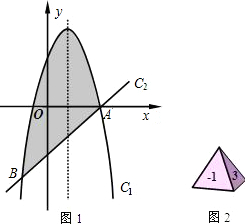，0）和点B．
（1）求a、b的值；
（2）若P（t，y₁），Q（2，y₂）是抛物线C₁上的两点，且y₁＜y₂，求实数t的取值范围；
（3）如图2，质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4．随机抛掷这枚骰子两次，把第一次着地一面的数字m记做P点的横坐标，第二次着地一面的数字n记做P点的纵坐标．则点P（m，n） 落在图1中抛物线C₁与直线C₂围成区域内（图中阴影部分，含边界）的概率是多少？

Answer 1

分析：（1）把A的坐标代入抛物线与直线的解析式即可求得a，b的值；
（2）首先求得y₂=3的值，然后抛物线上纵坐标是3的点的横坐标的值，根据抛物线的增减性即可确定；
（3）首先利用列举法求得所有的情况有几种，然后根据函数的值确定每个点是否在区域内．

解答：解：（1）把A（3，0）代入抛物线的解析式得：4a+4=0，解得：a=-1；
把（3，0）代入直线的解析式得：3+b=0，解得：b=-3；

（2）抛物线的解析式是：y=-（x-1）²+4．
在解析式中，令x=2，解得y₂=3．
在抛物线中，令y=3，解得：x=2或1．
则当t＜1或t＞3时，y₁＜y₂；

（3）解方程组：

y=-(x-1)2+4 y=x-3

，解得：x=3或-2
则B的横坐标是-2．
当点在阴影区域时，横坐标x满足：-2≤x≤3
P点的坐标用树形图表示：

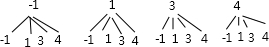
当x=-1时，代入抛物线的解析式得：y=0，代入直线的解析式得：y=-4．
故点（-1，-1）在区域内；
当x=1时，代入抛物线的解析式得：y=4，代入直线的解析式得：y=-2，则（1，-1）（1，1）（1，3）（1，4）在区域内；
当x=3时，代入抛物线解析式得：y=0，代入直线解析式得：y=0．
故在区域内的点有：（-1，-1），（1，-1）（1，1）（1，3）（1，4）．共5个．
则落在图1中抛物线C₁与直线C₂围成区域内（图中阴影部分，含边界）的概率是5÷16=

5

16

．

点评：本题主要考查了二次函数图象上的点的特点，以及列举法求概率，正确确定点是否在区域内是解题的关键．