ΧβΡΩΡΎ»ί
Θ®2013•Ρœ…≥«χ“ΜΡΘΘ©»γΆΦ1Θ§“―÷Σ≈ΉΈοœΏy=
x2+bx+c”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ§«“OB=2OA=4Θ°
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©…ηP «Θ®1Θ©÷–≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§“‘PΈΣ‘≤–ΡΘ§RΈΣΑκΨΕΉςΓ―PΘ§«σΒ±Γ―P”κ≈ΉΈοœΏΒΡΕ‘≥Τ÷αlΦΑx÷αΨυœύ«– ±ΒψPΒΡΉχ±ξΘ°
Θ®3Θ©Ε·ΒψE¥”ΒψA≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψB‘ΥΕ·Θ§Ε·ΒψF¥”ΒψB≥ωΖΔΘ§“‘ΟΩΟκ
ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψC‘ΥΕ·Θ§ΙΐΒψEΉςEGΓΈy÷αΘ§ΫΜAC”ΎΒψGΘ®»γΆΦ2Θ©Θ°»τEΓΔFΝΫΒψΆ§ ±≥ωΖΔΘ§‘ΥΕ· ±ΦδΈΣtΘ°‘ρΒ±tΈΣΚΈ÷Β ±Θ§ΓςEFGΒΡΟφΜΐ «ΓςABCΒΡΟφΜΐΒΡ
ΘΩ

| 1 |
| 2 |
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©…ηP «Θ®1Θ©÷–≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§“‘PΈΣ‘≤–ΡΘ§RΈΣΑκΨΕΉςΓ―PΘ§«σΒ±Γ―P”κ≈ΉΈοœΏΒΡΕ‘≥Τ÷αlΦΑx÷αΨυœύ«– ±ΒψPΒΡΉχ±ξΘ°
Θ®3Θ©Ε·ΒψE¥”ΒψA≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψB‘ΥΕ·Θ§Ε·ΒψF¥”ΒψB≥ωΖΔΘ§“‘ΟΩΟκ
| 2 |
| 1 |
| 3 |

Ζ÷ΈωΘΚΘ®1Θ©ΗυΨίOAΓΔOBΒΡ≥ΛΕ»«σ≥ωΒψAΓΔBΒΡΉχ±ξΘ§»ΜΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σΕΰ¥ΈΚ· ΐΫβΈω ΫΫβ¥πΘΜ
Θ®2Θ©ΗυΨί≈ΉΈοœΏΫβΈω Ϋ«σ≥ωΕ‘≥Τ÷αΈΣx=1Θ§≤ΔΗυΨί≈ΉΈοœΏΫβΈω Ϋ…η≥ωΒψPΒΡΉχ±ξΘ§»ΜΚσΗυΨίΒψPΒΫ÷±œΏx=1”κx÷αΒΡΨύάκœύΒ»Ν–≥ωΖΫ≥ΧΘ§‘ΌΫβΨχΕ‘÷ΒΖΫ≥ΧΦ¥Ω…ΒΟΫβΘΜ
Θ®3Θ©ΗυΨί≈ΉΈοœΏΫβΈω Ϋ«σ≥ωΒψCΒΡΉχ±ξΘ§»ΜΚσ«σ≥ωΓςABCΒΡΟφΜΐΘ§≤Δάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ“Μ¥ΈΚ· ΐΫβΈω Ϋ«σ≥ω÷±œΏACΒΡΫβΈω ΫΘ§≈–Εœ≥ωΓςBOC «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§»ΜΚσ”Οt±μ Ψ≥ωΒψEΒΡΉχ±ξΘ§¥”Εχ«σ≥ωEGΒΡ≥ΛΕ»Θ§ΙΐFΉςFMΓΆx÷α”ΎΒψMΘ§”Οt±μ Ψ≥ωBMΒΡ≥ΛΕ»Θ§»ΜΚσ”Οt±μ Ψ≥ωEMΒΡ≥ΛΕ»Θ§Φ¥ΓςEFG±ΏEG…œΒΡΗΏΘ§‘ΌΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΝ– Ϋ«σΫβΦ¥Ω…Θ°
Θ®2Θ©ΗυΨί≈ΉΈοœΏΫβΈω Ϋ«σ≥ωΕ‘≥Τ÷αΈΣx=1Θ§≤ΔΗυΨί≈ΉΈοœΏΫβΈω Ϋ…η≥ωΒψPΒΡΉχ±ξΘ§»ΜΚσΗυΨίΒψPΒΫ÷±œΏx=1”κx÷αΒΡΨύάκœύΒ»Ν–≥ωΖΫ≥ΧΘ§‘ΌΫβΨχΕ‘÷ΒΖΫ≥ΧΦ¥Ω…ΒΟΫβΘΜ
Θ®3Θ©ΗυΨί≈ΉΈοœΏΫβΈω Ϋ«σ≥ωΒψCΒΡΉχ±ξΘ§»ΜΚσ«σ≥ωΓςABCΒΡΟφΜΐΘ§≤Δάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ“Μ¥ΈΚ· ΐΫβΈω Ϋ«σ≥ω÷±œΏACΒΡΫβΈω ΫΘ§≈–Εœ≥ωΓςBOC «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§»ΜΚσ”Οt±μ Ψ≥ωΒψEΒΡΉχ±ξΘ§¥”Εχ«σ≥ωEGΒΡ≥ΛΕ»Θ§ΙΐFΉςFMΓΆx÷α”ΎΒψMΘ§”Οt±μ Ψ≥ωBMΒΡ≥ΛΕ»Θ§»ΜΚσ”Οt±μ Ψ≥ωEMΒΡ≥ΛΕ»Θ§Φ¥ΓςEFG±ΏEG…œΒΡΗΏΘ§‘ΌΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΝ– Ϋ«σΫβΦ¥Ω…Θ°
Ϋβ¥πΘΚΫβΘΚΘ®1Θ©ΓΏOB=2OA=4Θ§
ΓύOA=2Θ§
ΓύΒψAΘ®-2Θ§0Θ©Θ§BΘ®4Θ§0Θ©Θ§
Α―ΒψAΓΔBΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏy=
x2+bx+cΒΟΘ§
Θ§
ΫβΒΟ
Θ§
Γύ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣy=
x2-x-4ΘΜ
Θ®2Θ©≈ΉΈοœΏΕ‘≥Τ÷αΈΣx=-
=-
=1Θ§
…ηΒψPΉχ±ξΈΣΘ®xΘ§
x2-x-4Θ©Θ§
ΓΏΓ―P”κ≈ΉΈοœΏΒΡΕ‘≥Τ÷αlΦΑx÷αΨυœύ«–Θ§
Γύ|x-1|=|
x2-x-4|Θ§
Φ¥x-1=
x2-x-4ΔΌΜρx-1=-Θ®
x2-x-4Θ©ΔΎΘ§
ΫβΖΫ≥ΧΔΌΘ§’ϊάμΒΟΘ§x2-4x-6=0Θ§
ΫβΒΟx1=2+
Θ§x2=2-
Θ§
Β±x1=2+
±Θ§y1=2+
-1=1+
Θ§
Β±x2=2-
±Θ§y2=2-
-1=1-
Θ§
¥Υ ±ΒψPΒΡΉχ±ξΈΣΘ®2+
Θ§1+
Θ©ΜρΘ®2-
Θ§1-
Θ©Θ§
ΫβΖΫ≥ΧΔΎΘ§’ϊάμΒΟΘ§x2-10=0Θ§
ΫβΒΟx3=
Θ§x4=-
Θ§
Β±x3=
±Θ§y3=1-
Θ§
Β±x4=-
±Θ§y4=1+
Θ§
¥Υ ±Θ§ΒψPΒΡΉχ±ξΈΣΘ®
Θ§1-
Θ©ΜρΘ®-
Θ§1+
Θ©Θ§
Ήέ…œΥυ ωΘ§ΒψPΒΡΉχ±ξΈΣΘ®2+
Θ§1+
Θ©ΜρΘ®2-
Θ§1-
Θ©ΜρΘ®
Θ§1-
Θ©ΜρΘ®-
Θ§1+
Θ©ΘΜ
Θ®3Θ©≈ΉΈοœΏΫβΈω ΫΒ±x=0 ±Θ§y=-4Θ§
Υυ“‘Θ§ΒψCΒΡΉχ±ξΈΣΘ®0Θ§-4Θ©Θ§
”÷ΓΏAB=OA+OB=2+4=6Θ§
ΓύSΓςABC=
ΓΝ6ΓΝ4=12Θ§
…η÷±œΏACΒΡΫβΈω ΫΈΣy=kx+bΘ§‘ρ
Θ§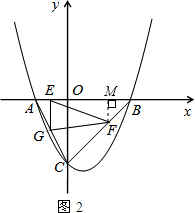
ΫβΒΟ
Θ§
Υυ“‘Θ§÷±œΏACΒΡΫβΈω ΫΈΣy=-2x-4Θ§
ΓΏΒψE¥”ΒψA≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψB‘ΥΕ·Θ§
ΓύAE=tΘ§ΒψEΒΡΉχ±ξΈΣΘ®-2+tΘ§0Θ©Θ§
ΓύEG=-2Θ®-2+tΘ©-4=-2tΘ§
ΓΏBΘ®4Θ§0Θ©Θ§CΘ®0Θ§-4Θ©Θ§
ΓύΓςBOC «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
»γΆΦΘ§ΙΐΒψFΉςFMΓΆx÷α”ΎΒψMΘ§
ΓΏΒψF¥”ΒψB≥ωΖΔΘ§“‘ΟΩΟκ
ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψC‘ΥΕ·Θ§
ΓύBF=
tȧ
ΓύBM=
ΓΝ
t=tȧ
ΓύME=AB-AE-BM=6-t-t=6-2tΘ§
Φ¥ΒψFΒΫEGΒΡΨύάκΈΣΘ®6-2tΘ©Θ§
ΓύSΓςEFG=
ΓΝ|-2t|ΓΝΘ®6-2tΘ©=-2t2+6tΘ§
”÷ΓςEFGΒΡΟφΜΐ «ΓςABCΒΡΟφΜΐΒΡ
Θ§
Γύ-2t2+6t=
ΓΝ12Θ§
’ϊάμΒΟΘ§t2-3t+2=0Θ§
ΫβΒΟt1=1Θ§t2=2Θ§
ΓύΒ±tΈΣ1ΟκΜρ2Οκ ±Θ§ΓςEFGΒΡΟφΜΐ «ΓςABCΒΡΟφΜΐΒΡ
Θ°
ΓύOA=2Θ§
ΓύΒψAΘ®-2Θ§0Θ©Θ§BΘ®4Θ§0Θ©Θ§
Α―ΒψAΓΔBΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏy=
| 1 |
| 2 |
|
ΫβΒΟ
|
Γύ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣy=
| 1 |
| 2 |
Θ®2Θ©≈ΉΈοœΏΕ‘≥Τ÷αΈΣx=-
| b |
| 2a |
| -1 | ||
2ΓΝ
|
…ηΒψPΉχ±ξΈΣΘ®xΘ§
| 1 |
| 2 |
ΓΏΓ―P”κ≈ΉΈοœΏΒΡΕ‘≥Τ÷αlΦΑx÷αΨυœύ«–Θ§
Γύ|x-1|=|
| 1 |
| 2 |
Φ¥x-1=
| 1 |
| 2 |
| 1 |
| 2 |
ΫβΖΫ≥ΧΔΌΘ§’ϊάμΒΟΘ§x2-4x-6=0Θ§
ΫβΒΟx1=2+
| 10 |
| 10 |
Β±x1=2+
| 10 |
| 10 |
| 10 |
Β±x2=2-
| 10 |
| 10 |
| 10 |
¥Υ ±ΒψPΒΡΉχ±ξΈΣΘ®2+
| 10 |
| 10 |
| 10 |
| 10 |
ΫβΖΫ≥ΧΔΎΘ§’ϊάμΒΟΘ§x2-10=0Θ§
ΫβΒΟx3=
| 10 |
| 10 |
Β±x3=
| 10 |
| 10 |
Β±x4=-
| 10 |
| 10 |
¥Υ ±Θ§ΒψPΒΡΉχ±ξΈΣΘ®
| 10 |
| 10 |
| 10 |
| 10 |
Ήέ…œΥυ ωΘ§ΒψPΒΡΉχ±ξΈΣΘ®2+
| 10 |
| 10 |
| 10 |
| 10 |
| 10 |
| 10 |
| 10 |
| 10 |
Θ®3Θ©≈ΉΈοœΏΫβΈω ΫΒ±x=0 ±Θ§y=-4Θ§
Υυ“‘Θ§ΒψCΒΡΉχ±ξΈΣΘ®0Θ§-4Θ©Θ§
”÷ΓΏAB=OA+OB=2+4=6Θ§
ΓύSΓςABC=
| 1 |
| 2 |
…η÷±œΏACΒΡΫβΈω ΫΈΣy=kx+bΘ§‘ρ
|

ΫβΒΟ
|
Υυ“‘Θ§÷±œΏACΒΡΫβΈω ΫΈΣy=-2x-4Θ§
ΓΏΒψE¥”ΒψA≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψB‘ΥΕ·Θ§
ΓύAE=tΘ§ΒψEΒΡΉχ±ξΈΣΘ®-2+tΘ§0Θ©Θ§
ΓύEG=-2Θ®-2+tΘ©-4=-2tΘ§
ΓΏBΘ®4Θ§0Θ©Θ§CΘ®0Θ§-4Θ©Θ§
ΓύΓςBOC «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
»γΆΦΘ§ΙΐΒψFΉςFMΓΆx÷α”ΎΒψMΘ§
ΓΏΒψF¥”ΒψB≥ωΖΔΘ§“‘ΟΩΟκ
| 2 |
ΓύBF=
| 2 |
ΓύBM=
| ||
| 2 |
| 2 |
ΓύME=AB-AE-BM=6-t-t=6-2tΘ§
Φ¥ΒψFΒΫEGΒΡΨύάκΈΣΘ®6-2tΘ©Θ§
ΓύSΓςEFG=
| 1 |
| 2 |
”÷ΓςEFGΒΡΟφΜΐ «ΓςABCΒΡΟφΜΐΒΡ
| 1 |
| 3 |
Γύ-2t2+6t=
| 1 |
| 3 |
’ϊάμΒΟΘ§t2-3t+2=0Θ§
ΫβΒΟt1=1Θ§t2=2Θ§
ΓύΒ±tΈΣ1ΟκΜρ2Οκ ±Θ§ΓςEFGΒΡΟφΜΐ «ΓςABCΒΡΟφΜΐΒΡ
| 1 |
| 3 |
ΒψΤάΘΚ±ΨΧβ «Εΰ¥ΈΚ· ΐΉέΚœΧβ–ΆΘ§÷ς“ΣΩΦ≤ιΝΥ¥ΐΕ®œΒ ΐΖ®«σΚ· ΐΫβΈω ΫΘ®Εΰ¥ΈΚ· ΐΫβΈω Ϋ”κ“Μ¥ΈΚ· ΐΫβΈω ΫΘ©Θ§÷±œΏ”κ‘≤œύ«–Θ§‘≤–ΡΒΫ÷±œΏΒΡΨύάκΒ»”Ύ‘≤ΒΡΑκΨΕΘ§Ϋβ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΘ§“‘ΦΑ»ΐΫ«–ΈΒΡΟφΜΐΘ§±ΨΧβΥΦ¬Ζ±»ΫœΗ¥‘”Θ§‘ΥΥψΝΩΫœ¥σΘ§“ΣΉΔ“βΖ÷«ιΩωΧ÷¬έ«σΫβΘ§ΦΤΥψ ±“Σ»œ’φΉ–œΗΘ°

ΝΖœΑ≤αœΒΝ–¥πΑΗ
œύΙΊΧβΡΩ
 Θ®2013•Ρœ…≥«χ“ΜΡΘΘ©»γΆΦΘ§“ΜΗωΩ’ΦδΦΗΚΈΧεΒΡ÷ς ”ΆΦΚΆΉσ ”ΆΦΕΦ «±Ώ≥ΛΈΣ2ΒΡ’ΐ»ΐΫ«–ΈΘ§Η© ”ΆΦ «“ΜΗω‘≤Θ§Ρ«Ο¥’βΗωΦΗΚΈΧεΒΡ≤ύΟφΜΐ «
Θ®2013•Ρœ…≥«χ“ΜΡΘΘ©»γΆΦΘ§“ΜΗωΩ’ΦδΦΗΚΈΧεΒΡ÷ς ”ΆΦΚΆΉσ ”ΆΦΕΦ «±Ώ≥ΛΈΣ2ΒΡ’ΐ»ΐΫ«–ΈΘ§Η© ”ΆΦ «“ΜΗω‘≤Θ§Ρ«Ο¥’βΗωΦΗΚΈΧεΒΡ≤ύΟφΜΐ «