题目内容
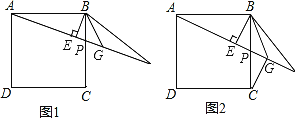
【题目】已知如图1,P为正方形ABCD的边BC上任意一点,BE⊥AP于点E,在AP的延长线上取点F,使EF=AE,连接BF,∠CBF的平分线交AF于点G.
(1)求证:BF=BC;
(2)求证:△BEG是等腰直角三角形;
(3)如图2,若正方形ABCD的边长为4,连接CG,当P点为BC的中点时,求CG的长.
【答案】(1)证明见解析;92)证明见解析;(3)![]()
【解析】(1)利用线段的垂直平分线的性质以及正方形的性质即可证明;
(2)想办法证明∠F=∠BAF=∠EBP,由∠EBG=∠EBP+∠PBG,∠EGB=∠F+∠GBF,即可解决问题;
(3)求出BG,只要证明△EBP≌△GCP,即可推出CG=BE,由此即可解决问题.
解:(1)证明:∵BE⊥AP,AE=EF,
∴BE垂直平分线段AF,
∴AB=BF,
在正方形ABCD中,AB=BC,
∴BF=BC;
(2)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠EBP=90°,
∵BE⊥AF,
∴∠ABE+∠BAP=90°,
∴∠BAP=∠EBP,
∵AB=BF∴∠BAP=∠BFP,
∴∠EBP=∠BFP,
∵∠CBF的平分线交AF于点G,
∴∠CBG=∠FBG,
∴∠EBP+∠CBG=∠BFP+∠FBG,
∴∠EBG=∠EGB,
∵BE⊥AF,
∴△BEG是等腰直角三角形.
(3)解:∵P是BC的中点,正方形的边长为4,
∴AB=4,BP=CP=2,
∵在Rt△ABP中,
∴AP=![]() ,
,
∵BE⊥AP,
∴S△ABP=![]() ,
,
解得:BE=![]() ,
,
∵AB=BC,AB=BF,
∴BC=BF,
由(1)可知∠CBG =∠FBG,
∴BG=BG,
∴△CBG≌△FBG,
∴∠BFP=∠BCG,
由(2)可知∠EBP=∠BFP,
∴∠EBP =∠BCG∵∠EPB =∠CPG,
∴△EBP≌△GCP,
∴CG=BE=![]() .
.
“点睛”本题考查正方形到现在、全等三角形的判定和性质、相等的垂直平分线的性质、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考压轴题.