题目内容
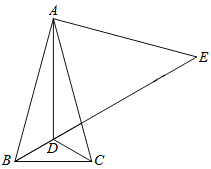
【题目】如图,在△ABC中,AB=AC,∠BAC=30°,点D是△ABC内一点,DB=DC,∠DCB=30°,点E是BD延长线上一点,AE=AB.
(1)求∠ADE的度数;
(2)求证:DE=AD+DC;
【答案】(1)60°;(2)见解析
【解析】试题分析:(1)△ABC中,AB=AC,∠BAC=30°,根据等腰三角形的性质和三角形的内角和定理可得∠ABC=∠ACB=75°,由DB=DC,∠DCB=30°,根据等腰三角形的性质再求得∠DBC=∠DCB=30°,即可得∠ABD=45°,易证AD所在直线垂直平分BC,根据等腰三角形的三线合一的性质可得AD平分∠BAC,即可求得∠BAD=15°,利用三角形外角的性质即可求得∠ADE=60°;(2)如图1,在线段DE上截取DM=AD,连接AM,证明△ABD≌△AEM,根据全等三角形的对应边相等和线段的和差即可证得结论.
试题解析:
(1)∵△ABC中,AB=AC,∠BAC=30°,
∴∠ABC=∠ACB=![]() =75°,∵DB=DC,∠DCB=30°,∴∠DBC=∠DCB=30°,
=75°,∵DB=DC,∠DCB=30°,∴∠DBC=∠DCB=30°,
∴∠ABD=∠ABC﹣∠DBC=45°,∵AB=AC,DB=DC,∴AD所在直线垂直平分BC,
∴AD平分∠BAC,∴∠BAD=![]() ∠BAC=15°,∴∠ADE=∠ABD+∠BAD=60°;
∠BAC=15°,∴∠ADE=∠ABD+∠BAD=60°;
(2)如图1,在线段DE上截取DM=AD,连接AM,
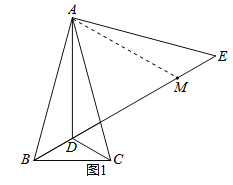
∵∠ADE=60°,DM=AD,
∴△ADM是等边三角形,∴∠ADB=∠AME=120°
∵AE=AB,∴∠ABD=∠E,
在△ABD和△AEM中,
∠ADB=∠AME,∠ABD=∠E,AB=AE,
∴△ABD≌△AEM(AAS),
∴BD=ME,∵BD=CD,∴CD=ME,
∵DE=DM+ME,∴DE=AD+CD.

练习册系列答案
相关题目