Question

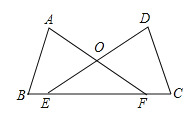
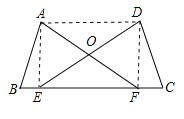
【题目】如图，四边形内接于半径为的中，连接，若，，则的长度为（ ）

A.B.C.D.

Answer 1

【答案】A

【解析】

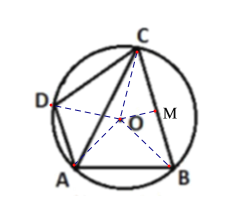
连接OA，OB，OC，OD，过点O作OM⊥BC于点M，易得∠AOB=∠COD=90°，∠DAC=∠ACB=45°，从而得∠OAD=∠CAB，进而得∠OAD=∠AOD，可得∠AOD=60°，∠BOC=120°，进而即可求解．

连接OA，OB，OC，OD，过点O作OM⊥BC于点M，

∵在四边形内接于半径为的中，，

∴∠AOB=∠COD=2∠ACB=90°，∠DAC=∠ACB=45°，

∵OA=OB，

∴∠OAB=45°，

∴∠OAD=∠DAC+∠CAO=∠OAB+∠CAO=∠CAB，

又∵∠ACD=∠AOD，，

∴∠AOD=∠BAC，

∴∠OAD=∠AOD，

∴AD=OD，

∵OD=OA，

∴AOD是等边三角形，

∴∠AOD=60°，

∴∠BOC=360°-90°-90°-60°=120°，

∵OC=OC=6，

∴∠OCM=30°，

∴CM=OC=3，

∴BC=2 CM==6．

故选A．