Question

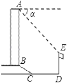
【题目】如图，在Rt△ABC中，∠C=90°，AC=2，BC=4，AC∥x轴，A、B两点在反比例函数y=（x＞0）的图象上，延长CA交y轴于点D，AD=1．

（1）求该反比例函数的解析式；

（2）将△ABC绕点B顺时针旋转得到△EBF，使点C落在x轴上的点F处，点A的对应点为E，求旋转角的度数和点E的坐标．

Answer 1

【答案】(1) y=；(2) 旋转角为120°, E点坐标为（2+，）

【解析】

（1）设A（1，k），再表示出B（3，k-4），则利用反比例函数图象上点的坐标特征得到3（k-4）=k，解方程求出k即可得到该反比例函数的解析式；
（2）作BM⊥x轴于M，EN⊥x轴于N，如图，根据旋转的性质得BF=BC=4，EF=AC=2，∠BFE=∠BCA=90°，∠CBF等于旋转角，再计算出BM=CM-BC=2，则在Rt△BMF中，利用三角函数可求出∠MBF=60°，MF=,BM=，于是得到旋转角为120°，然后证明Rt△BMF∽Rt△FNE，利用相似比求出FN和EN，从而可得到E点坐标．

解：（1）∵AC∥x轴，AD=1，

∴A（1，k），

∵∠C=90°，AC=2，BC=4，

∴B（3，k﹣4），

∵点B在y=的图象上，

∴3（k﹣4）=k，解得k=6，

∴该反比例函数的解析式为y=；

（2）作BM⊥x轴于M，EN⊥x轴于N，如图，

∵△ABC绕点B顺时针旋转得到△EBF，

∴BF=BC=4，EF=AC=2，∠BFE=∠BCA=90°，∠CBF等于旋转角，

∵BC⊥x轴，A（1，6），

∴BM=CM﹣BC=6﹣4=2，

在Rt△BMF中，∵cos∠MBF===，

∴∠MBF=60°，MF=BM=，

∴∠CBF=180°﹣∠MBF=120°，

∴旋转角为120°；

∵∠BFM+∠MBF=90°，∠BFM+∠EFN=90°，

∴∠MBF=∠EFN，

∴Rt△BMF∽Rt△FNE，

∴==，即==，

∴FN=1，EN=，

∴ON=OM+MF+FN=1++1=2+，

∴E点坐标为（2+，）．