题目内容

如图所示，已知二次函数经过、、C三点，点是抛物线与直线的一个交点．
（1）求二次函数关系式和点C的坐标；
（2）对于动点，求的最大值；
（3）若动点M在直线上方的抛物线运动，过点M做x轴的垂线交x轴于点F，如果直线AP把线段MF分成1:2的两部分，求点M的坐标。

（1）函数关系式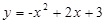：; C点坐标为（0,3）
（2）
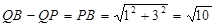
（3）M的坐标为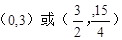

解析试题分析：(1)本题考查的是二次函数的性质以及待定系数法求二次函数解析式的相关知识，我们要注意根据已知条件选择合适的关系式的设法，本题利用一般式，由于已知常数项，再把两点坐标代入关系式，得到关于a、b的二元一次方程组，解方程组求出a、b的值，关系式便可得出.C点坐标为（0,3）(2)把函数关系式写成顶点式的形式后，可以知道动点在二次函数的对称轴上，只有当Q、P、B三点共线时，的值最大.(3)由于点M、E都在x轴上方，MF∥y轴，ME=yM-yE  EF=yE MF=yM  线段MF分成1:2的两部分注意有两种情况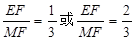，见题解.
试题解析：解（1）把两点坐标代入关系式得a=-1,b=2
∴函数关系式为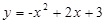.由函数关系式得C点坐标为（0,3）.
（2）如图：因为，所以动点Q（1，n)在二次函数的对称轴上。 所以当点Q、P、B三点共线时，的值最大，最大值为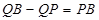
把x=2代入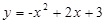，得y=3
即点P的坐标为（2,3）,又因为B（3,0）
所以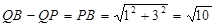
（3）因为点P坐标为（2，3）代入得k=1
所以直线l的关系式为：y=x+1
因为AP把线段MF分成1:2的两部分，
则根据题意，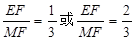
设点M的横坐标为x，那么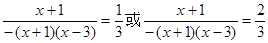

解得x=0或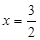
代入y=x+1得：y=3或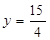
所以点M的坐标为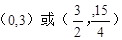
考点：1、待定系数法求二次函数解析式；2、二次函数的图象；3、平面直角坐标系中线段的长度的表示方法；4、三点共线时，两线段之差是最大值.

练习册系列答案
相关题目

如图1、2，已知四边形ABCD为正方形，在射线AC上有一动点P，作PE⊥AD（或延长线）于E，作PF⊥DC（或延长线）于F，作射线BP交EF于G．
（1）在图1中，设正方形ABCD的边长为2，四边形ABFE的面积为y，AP=x，求y关于x的函数表达式；
（2）结论：GB⊥EF对图1，图2都是成立的，请任选一图形给出证明；
（3）请根据图2证明：△FGC∽△PFB．

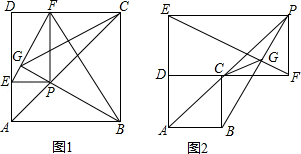
定义1：在△ABC中，若顶点A，B，C按逆时针方向排列，则规定它的面积为“有向面积”；若顶点A，B，C按顺时针方向排列，则规定它的面积的相反数为△ABC的“有向面积”.“有向面积”用表示，例如图1中，，图2中，.
定义2：在平面内任取一个△ABC和点P（点P不在△ABC的三边所在直线上），称有序数组（，，）为点P关于△ABC的“面积坐标”，记作，例如图3中，菱形ABCD的边长为2，，则，点G关于△ABC的“面积坐标”为.在图3中，我们知道，利用“有向面积”，我们也可以把上式表示为：.
应用新知：
（1）如图4，正方形ABCD的边长为1，则        ，点D关于△ABC的“面积坐标”是       ；探究发现：
（2）在平面直角坐标系中，点，
①若点P是第二象限内任意一点（不在直线AB上），设点P关于的“面积坐标”为，
试探究与之间有怎样的数量关系，并说明理由；
②若点是第四象限内任意一点，请直接写出点P关于的“面积坐标”（用x,y表示）；
解决问题：
（3）在（2）的条件下，点，点Q在抛物线上，求当的值最小时，点Q的横坐标.

抛物线（b，c均为常数）与x轴交于两点，与y轴交于点．
（1）求该抛物线对应的函数表达式；
（2）若P是抛物线上一点，且点P到抛物线的对称轴的距离为3，请直接写出点P的坐标．

如图，抛物线y=x²+bx+c与直线y=x－1交于A、B两点.点A的横坐标为－3，点B在y轴上，点P是y轴左侧抛物线上的一动点，横坐标为m，过点P作PC⊥x轴于C，交直线AB于D.
（1）求抛物线的解析式；
（2）当m为何值时，；
（3）是否存在点P,使△PAD是直角三角形，若存在，求出点P的坐标；若不存在，说明理由.

若两个二次函数图象的顶点，开口方向都相同，则称这两个二次函数为“同簇二次函数”。
（1）请写出两个为“同簇二次函数”的函数；
（2）已知关于x的二次函数y1=2x2—4mx+2m2+1，和y2=ax2+bx+5，其中y1的图象经过点A（1，1），若y1+y2为y1为“同簇二次函数”，求函数y2的表达式，并求当0≤x≤3时，y2的最大值。

如图，抛物线与x轴交于A（5,0）、B（-1,0）两点，过点A作直线AC⊥x轴，交直线于点C；
（1）求该抛物线的解析式；
（2）求点A关于直线的对称点的坐标，判定点是否在抛物线上，并说明理由；
（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.

如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，且对称轴为x=1，点A坐标为（-1，0）．则下面的四个结论：
①2a+b=0；②4a+2b+c＞0；③B点坐标为（4，0）；④当x＜-1时，y＞0．
其中正确的是（　　）
A．①②      B．③④      C．①④      D．②③

如图，在平面直角坐标系中，已知点A、B、C在x轴上，点D、E在y轴上，OA＝OD＝2，OC＝OE＝4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点（点P与F、G不重合），作PQ∥y轴与抛物线交于点Q．
（1）若经过B、E、C三点的抛物线的解析式为y＝－x2＋（2b－1）x＋c－5，则b＝         ，c＝         （直接填空）
（2）①以P、D、E为顶点的三角形是直角三角形，则点P的坐标为         （直接填空）
②若抛物线顶点为N，又PE＋PN的值最小时，求相应点P的坐标.
（3）连结QN，探究四边形PMNQ的形状：
①能否成为平行四边形
②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网