Question

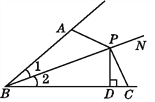
【题目】如图,∠1=∠2,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.试说明:∠BAP+∠BCP=180°.

Answer 1

【答案】见解析

【解析】作PE垂直于AB于E，根据角平分线的性质可知PD=PE，HL定理可知△PBD≌△PBE，可得BD=BE，根据题中线段和差的关系，可得△PAE≌△PCD，所以可知∠PAE=∠PCD，根据∠PAE+∠PAB=180°，即可证明题中关系.

证明：如图，过点P作PE⊥BA于E.

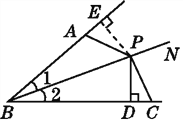
∵PD⊥BC，PE⊥BM，∠1=∠2，

∴PD=PE.

∵PD⊥BC，PE⊥BM，PD=PE，BP=BP，

∴△BPD≌△BPE.

∴BE=BD.

∵AB+BC=2BD，BC=BD+DC，AB=BE-AE，

∴AE=CD.

∵PD=PE，AE=CD，PD⊥BC，PE⊥BM，

∴△PCD≌△PAE，

∴∠PCB=∠PAE.

∵∠BAP+∠PAE=180°，

∴∠BAP+∠PCB=180°.