题目内容
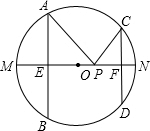 如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为多少?
如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为多少?分析:由于A、B两点关于MN对称,因而PA+PC=PB+PC,即当B、C、P在一条直线上时,PA+PC的最小,即BC的值就是PA+PC的最小值.
解答: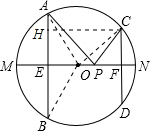 解:连接OA,OB,OC,作CH垂直于AB于H.
解:连接OA,OB,OC,作CH垂直于AB于H.
∵AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,
∴BE=
AB=4,CF=
CD=3,
∴OE=
=
=3,
OF=
=
=4,
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在Rt△BCH中根据勾股定理得到BC=
=
=7
,即PA+PC的最小值为7
.
 解:连接OA,OB,OC,作CH垂直于AB于H.
解:连接OA,OB,OC,作CH垂直于AB于H.∵AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=
| OB2-BE2 |
| 52-42 |
OF=
| OC2-CF2 |
| 52-32 |
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在Rt△BCH中根据勾股定理得到BC=
| BH2+CH2 |
| 72+72 |
| 2 |
| 2 |
点评:本题考查的是轴对称-最短路线问题,熟知“两点之间线段最短”是解答此题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
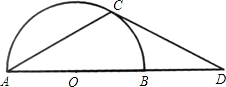 如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.
如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.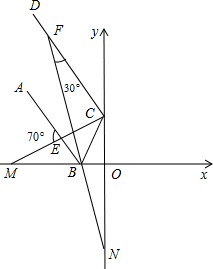
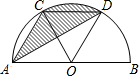 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.
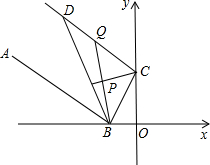
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R. (2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.
(2012•武汉模拟)如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.