题目内容
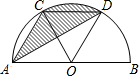 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为R.(1)CD与AB平行吗?为什么?
(2)求阴影部分的面积.
分析:(1)根据在同圆或等圆中,等弧所对的圆周角相等,根据内错角相等,两直线平行;
(2)根据同底等高的两个三角形的面积相等,则阴影部分的面积等于扇形OCD的面积.
(2)根据同底等高的两个三角形的面积相等,则阴影部分的面积等于扇形OCD的面积.
解答:解:(1)∵AB是半⊙O的直径,C、D是半圆的三等分点,
∴∠COD=∠AOC=∠BOD=60°,
∵OC=OD,
∴△OCD是等边三角形,
∴∠ODC=60°,
∴∠ODC=∠BOD,
∴CD∥AB;
(2)∵CD∥AB,
∴S△ACD=S△OCD,
∴S阴影=S扇形OCD=
=
πR2.
∴∠COD=∠AOC=∠BOD=60°,
∵OC=OD,
∴△OCD是等边三角形,
∴∠ODC=60°,
∴∠ODC=∠BOD,
∴CD∥AB;
(2)∵CD∥AB,
∴S△ACD=S△OCD,
∴S阴影=S扇形OCD=
| nπR2 |
| 360 |
| 1 |
| 6 |
点评:本题考查了扇形面积的计算以及圆周角定理,是基础知识要熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.
如图,AB是半⊙O的直径,弦AC与AB成30°的角,AC=CD.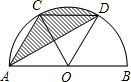 如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为4.阴影部分的面积为
如图,AB是半⊙O的直径,C、D是半圆的三等分点,半圆的半径为4.阴影部分的面积为 (2012•密云县二模)如图,AB是半⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为( )
(2012•密云县二模)如图,AB是半⊙O的直径,C是⊙O上一点,OD⊥BC于D,若AC:BC=4:3,AB=10cm,则OD的长为( ) 如图,AB是半⊙O的直径,点C是半⊙O的三等分点,设扇形AOC、△COB、弓形BPC的面积分别为S1、S2、S3,则它们的大小关系为
如图,AB是半⊙O的直径,点C是半⊙O的三等分点,设扇形AOC、△COB、弓形BPC的面积分别为S1、S2、S3,则它们的大小关系为