题目内容
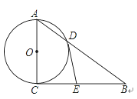
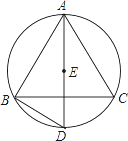
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.
(1)当△ABC的外接圆半径为1时,且∠BAC=60°,求弧BC的长度.
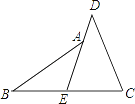
(2)连接BD,求证:DE=DB.
【答案】(1)![]() (2)详见解析.
(2)详见解析.
【解析】
(1)设△ABC的外接圆的圆心为O,连接OB、OC,由圆周角定理得出∠BOC=120°,再由弧长公式即可得出结果;
(2)连接BE,由三角形的内心得出∠1=∠2,∠3=∠4,再由三角形的外角性质和圆周角定理得出∠DEB=∠DBE,即可得出结论.
(1)解:设△ABC的外接圆的圆心为O,连接OB、OC,如图1所示:
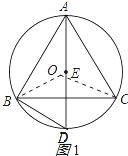
∵∠BAC=60°,
∴∠BOC=120°,
∴弧BC的长度=![]() =
=![]() .
.
(2)证明:连接BE,如图2所示:
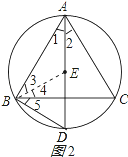
∵E是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∵∠DEB=∠1+∠3,∠DBE=∠4+∠5
∠5=∠2,
∴∠DEB=∠DBE,
∴DE=DB.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目