题目内容
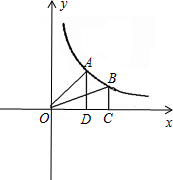如图，已知A、B是反比例函数y=| 1 |
| x |
| A、2：1 | B、1：2 |
| C、1：1 | D、2：3 |
分析：根据反比例函数比例系数k的几何意义可以得到三角形ADO和三角形BCO的面积相等，并据此求得三角形AOE的面积等于四边形BEDC的面积，表示出两个多边形的面积即可求解．
解答：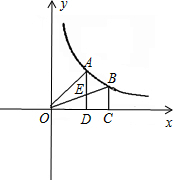
解：∵A、B是反比例函数y=
（x＞0）的图象上任意两点，
∴S△AOD=S△BOD，
∴S△AOE=S四边形BEDC，
∴S△AOD=S△BOD，
∴S△AOE+S△AEB=S△AEB+S四边形BEDC，
即：S△AOB=S梯形ADCB
∴梯形ABCD的面积与△ABO的面积比是1：1．
故选C
解：∵A、B是反比例函数y=| 1 |
| x |
∴S△AOD=S△BOD，
∴S△AOE=S四边形BEDC，
∴S△AOD=S△BOD，
∴S△AOE+S△AEB=S△AEB+S四边形BEDC，
即：S△AOB=S梯形ADCB
∴梯形ABCD的面积与△ABO的面积比是1：1．
故选C
点评：本题考查了反比例函数比例系数的几何意义，解题的关键要熟记系数k与三角形的面积的关系．
练习册系列答案
相关题目
如图，已知平行四边形ABCD，E是对角线AC延长线上的一点，
判断下列命题的真假，并给出证明（若是真命题给出证明，若是假命题举出反例）：
（1）如图，EF∥AD，∠1=∠2，∠BAC=70°，将求∠AGD的过程填写完整．
时，则称△A1B1C1与△A2B2C2有一定的“全等度”．如图，已知梯形ABCD，AD∥BC，∠B=30°，∠BCD=60°，连接AC．