题目内容
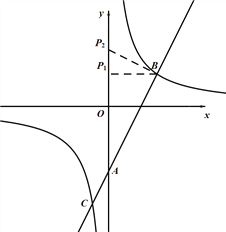
【题目】如图，在平面直角坐标系中，一次函数y1=ax+b（a≠0）的图象与y轴相交于点A，与反比例函数y2=
（c≠0）的图象相交于点B（3，2）、C（﹣1，n）．
（1）求一次函数和反比例函数的解析式；
（2）根据图象，直接写出y1＞y2时x的取值范围；
（3）在y轴上是否存在点P，使△PAB为直角三角形？如果存在，请求点P的坐标；若不存在，请说明理由．
【答案】（1）反比例函数解析式为： 
，一次函数解析式为y1=2x﹣4；（2）由图可知，当写出y1＞y2时x的取值范围是﹣1＜x＜0或者x＞3；（3）y轴上存在点P，使△PAB为直角三角形，P1（0，2）、P2（0， 
）．
【解析】试题分析：(1) 把B（3，2）代入
求得k的值，即可得反比例函数解析式，把C（－1，n）代入反比例函数的解析式，求得n值，再利用待定系数法求一次函数的解析式即可；（2）观察图象，直接写出结论即可；（3）
轴上存在点P，使△PAB为直角三角形，分∠B PA=90°和∠P BA=90°两种情况求点P的坐标即可.
试题解析：
（1）把B（3,2）代入
得： 
=6
∴反比例函数解析式为： 
把C（－1，n）代入
，得：n=－6
∴C（－1，－6）
把B（3,2）、C（－1，－6）分别代入
，得：
，解得： 
所以一次函数解析式为
（2）由图可知，当写出
>
时
的取值范围是－1＜
<0或者
>3
（3）
轴上存在点P，使△PAB为直角三角形
过B作BP1⊥
轴于P1
∠B P1 A=90°，△P1AB为直角三角形
此时，P1（0,2）
过B作BP2⊥AB交
轴于P2
∠P2 BA=90°，△P2 AB为直角三角形
在Rt△P1AB中，
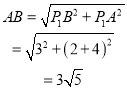
在Rt△P1 AB和Rt△P2 AB
∴
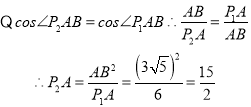
∴P2（0, 
）
综上所述，P1（0,2）、P2（0, 
）
练习册系列答案
相关题目
