Question

【题目】如图，已知直线与轴、轴分别相交于点、点，，若将沿直线折叠，使点与点重合，折痕与轴交于点，与交于点．

（1）求的值；

（2）求点的坐标；

（3）求直线的表达式．

Answer 1

【答案】(1) ；(2)； (3)

【解析】

(1)先求得点B的坐标，得到2，再根据角所对直角边等于斜边一半结合勾股定理即可求得的长，从而求得答案；

(2)根据折叠的性质可证得BC=AC，设，则，在中，利用勾股定理即可求得答案；

(3)点D时AB的中点，则点D(3，)，将点C、D的坐标代入一次函数表达式，即可求解．

(1)令，则，即：2，

∵，

∴4，

∴，

∴点的坐标为，

将代入得：，

∴；

(2)根据折叠的性质得：，

设，则，

∴在中，，即，

解得：，则，

则点C的坐标为：；

(3)根据折叠的性质知：点D是AB的中点，则点D的坐标为，

将点C、D的坐标代入一次函数的解析式得：，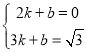

解得，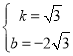

故直线CD的表达式为：．