题目内容
【题目】在一次机器人测试中，要求机器人从A出发到达B处．如图1，已知点A在O的正西方600cm处，B在O的正北方300cm处，且机器人在射线AO及其右侧（AO下方）区域的速度为20cm/秒，在射线AO的左侧（AO上方）区域的速度为10cm/秒．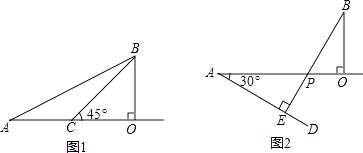 
（参考数据： 
≈1.414， 
≈1.732， 
≈2.236， 
≈2.449）
（1）分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间（精确到秒）；
（2）若∠OCB=45°，求机器人沿A→C→B路线到达B处所用的时间（精确到秒）；
（3）如图2，作∠OAD=30°，再作BE⊥AD于E，交OA于P．试说明：从A出发到达B处，机器人沿A→P→B路线行进所用时间最短．
【答案】
（1）解：沿A→O→B路线行进所用时间为：600÷20+300÷10=60（秒），
在Rt△OBA中，由勾股定理，得AB= 
=300 
（cm）．
∴沿A→B路线行进所用时间为：300 ÷10≈300×2.236÷10≈67（秒）
（2）解：在Rt△OBC中，OB=300，∠OCB=45°，∴OC=OB=300cm，BC= 
=300 
（cm），
∴AC=600﹣300=300（cm）．
∴沿A→C→B路线行进所用时间为：AC÷20+BC÷10=300÷20+300 ÷10≈15+42.42≈57（秒）
（3）解：在AO上任取异于点P的一点P′，作P′E′⊥AD于E′，连接P′B，
在Rt△APE和Rt△AP′E′中，sin30°= 
= 
，∴EP= 
，E′P′= 
．
∴沿A→P→B路线行进所用时间为：AP÷20+PB÷10=EP÷10+PB÷10=（EP+PB）÷10= 
BE（秒），
沿A→P′→B路线行进所用时间为：
AP′÷20+P′B÷10=E′P′÷10+P′B÷10=（E′P′+P′B）÷10= （E′P′+P′B）（秒）．
连接BE′，则E′P′+P′B＞BE′＞BE，∴ BE＜ （E′P′+P′B）．
∴沿A→P→B路线行进所用时间，小于沿A→P′→B路线行进所用时间．
即机器人沿A→P→B路线行进所用时间最短
【解析】（1）根据已知先求出沿A→O→B路线行进所用时间，然后由勾股定理求出AB，从而求出沿A→B路线行进所用时间；（2）首先解Rt△OBC，运用三角函数求出BC，继而得出AC，从而求出沿A→C→B路线到达B处所用的时间；（3）在AO上任取异于点P的一点P′，作P′E′⊥AD于E′，连接P′B，分别求出沿A→P→B路线行进所用时间和沿A→P′→B路线行进所用时间进行比较得出结论．
【考点精析】根据题目的已知条件，利用等腰直角三角形和含30度角的直角三角形的相关知识可以得到问题的答案，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．
