题目内容
(2009•台州模拟)在△ABC中,∠A=90°,AB=8cm,AC=6cm,点M,点N同时从点A出发,点M沿边AB以4cm/s的速度向点B运动,点N从点A出发,沿边AC以3cm/s的速度向点C运动,(点M不与A,B重合,点N不与A,C重合),设运动时间为xs.(1)求证:△AMN∽△ABC;
(2)当x为何值时,以MN为直径的⊙O与直线BC相切?
(3)把△AMN沿直线MN折叠得到△MNP,若△MNP与梯形BCNM重叠部分的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?

【答案】分析:(1)欲证△AMN∽△ABC,可以通过应用两组对应边的比相等且相应的夹角相等的两个三角形相似,(AM:AN=AB:AC=4:3,∠A=∠A)得出;
(2)MN为直径的⊙O与直线BC相切,则圆心O到直线BC的距离等于半径,列出函数关系式,求出x的值;
(3)因为∠A=90°,△MNP与梯形BCNM重叠部分的面积分为两种情况:等于S△PMN,或等于S△MNP-S△PEF,列出y关于x的函数表达式,求出当 时,y值最大,最大值是8.
时,y值最大,最大值是8.
解答: (1)证明:∵
(1)证明:∵ ,∠A=∠A,
,∠A=∠A,
∴△AMN∽△ABC.(4分)
(2)解:在Rt△ABC中,BC=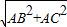 =10.
=10.
由(1)知△AMN∽△ABC.
∴
∴MN=5x,
∴⊙O的半径r=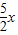
可求得圆心O到直线BC的距离d=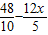
∵⊙O与直线BC相切
∴ =
= .解得x=
.解得x=
当x= 时,⊙O与直线BC相切.(8分)
时,⊙O与直线BC相切.(8分)
(3)解:当P点落在直线BC上时,则点M为AB的中点.(9分)
故以下分两种情况讨论:
①当0<x≤1时,y=S△PMN=6x2,
∴当x=1时,y最大=6×12=6.(11分)
②当1<x<2时,设MP交BC于E,NP交BC于F
MB=8-4x,MP=MA=4x
∴PE=4x-(8-4x)=8x-8
y=S△MNP-S△PEF= =
= (13分)
(13分)
∴当 时,y最大=8.
时,y最大=8.
综上所述,当 时,y值最大,最大值是8.(14分)
时,y值最大,最大值是8.(14分)
点评:考查了相似三角形的判断,结合切线的性质,及三角形的性质考查二次函数的综合应用.
(2)MN为直径的⊙O与直线BC相切,则圆心O到直线BC的距离等于半径,列出函数关系式,求出x的值;
(3)因为∠A=90°,△MNP与梯形BCNM重叠部分的面积分为两种情况:等于S△PMN,或等于S△MNP-S△PEF,列出y关于x的函数表达式,求出当
 时,y值最大,最大值是8.
时,y值最大,最大值是8.解答:
 (1)证明:∵
(1)证明:∵ ,∠A=∠A,
,∠A=∠A,∴△AMN∽△ABC.(4分)
(2)解:在Rt△ABC中,BC=
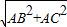 =10.
=10.由(1)知△AMN∽△ABC.
∴

∴MN=5x,
∴⊙O的半径r=
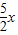
可求得圆心O到直线BC的距离d=
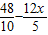
∵⊙O与直线BC相切
∴
 =
= .解得x=
.解得x=
当x=
 时,⊙O与直线BC相切.(8分)
时,⊙O与直线BC相切.(8分)(3)解:当P点落在直线BC上时,则点M为AB的中点.(9分)
故以下分两种情况讨论:
①当0<x≤1时,y=S△PMN=6x2,
∴当x=1时,y最大=6×12=6.(11分)
②当1<x<2时,设MP交BC于E,NP交BC于F
MB=8-4x,MP=MA=4x
∴PE=4x-(8-4x)=8x-8
y=S△MNP-S△PEF=
 =
= (13分)
(13分)∴当
 时,y最大=8.
时,y最大=8.综上所述,当
 时,y值最大,最大值是8.(14分)
时,y值最大,最大值是8.(14分)点评:考查了相似三角形的判断,结合切线的性质,及三角形的性质考查二次函数的综合应用.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 ,求弦AD的长.
,求弦AD的长.

 ,其中
,其中 .
.