题目内容
【题目】矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.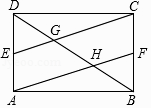
求证:
(1)四边形AFCE是平行四边形;
(2)证明:EG=FH.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴AD//BC,AD=BC,
∵E、F分别是AD、BC的中点,
∴AE= ![]() AD,CF=
AD,CF= ![]() BC,
BC,
∴AE![]() CF,
CF,
∴四边形AFCE是平行四边形;
(2)
证明:∵四边形AFCE是平行四边形,
∴CE//AF,
∴∠DGE=∠AHD=∠BHF,
∵AB//CD,
∴∠EDG=∠FBH,
在△DEG和△BFH中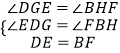 ,
,
∴△DEG≌△BFH(AAS),
∴EG=FH.
【解析】(1)根据一组对边平行且相等的四边形是平行四边形证明即可;
(2)可证明EG和FH所在的△DEG、△BFH全等即可.
【考点精析】本题主要考查了平行四边形的判定与性质和矩形的性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目