��Ŀ����
����Ŀ������δ֪��Ϊ x��y �Ķ�Ԫһ�η����飬���������Ľ� x��y ����![]() �����Ǿ�˵������Ľ� x �� y �������ںù�ϵ����
�����Ǿ�˵������Ľ� x �� y �������ںù�ϵ����
(1) ������![]() �Ľ�x��y�Ƿ�������ںù�ϵ��? ˵��������ɣ�
�Ľ�x��y�Ƿ�������ںù�ϵ��? ˵��������ɣ�
(2) ��������![]() �Ľ�x��y�������ںù�ϵ������m��ֵ��
�Ľ�x��y�������ںù�ϵ������m��ֵ��
(3) δ֪��Ϊx��y�ķ�����![]() ������a��x��y�������������÷�����Ľ�x��y�Ƿ�������ںù�ϵ��? ������У������a��ֵ��������Ľ⣻��������У���˵�����ɣ�
������a��x��y�������������÷�����Ľ�x��y�Ƿ�������ںù�ϵ��? ������У������a��ֵ��������Ľ⣻��������У���˵�����ɣ�
���𰸡�(1)��������Ľ�x,y�������ںù�ϵ�� ��(2)m=6��m=4��(3)a=1,������Ľ�Ϊ![]() .
.
��������
��1�������������![]() �Ľ⣬�ٸ������ںù�ϵ���Ķ����жϼ�����
�Ľ⣬�ٸ������ںù�ϵ���Ķ����жϼ�����
��2���ú�m�Ĵ���ʽ��ʾ��������![]() �Ľ⣬Ȼ�����
�Ľ⣬Ȼ�����![]() �з�����⣻
�з�����⣻
��3���ú�a�Ĵ���ʽ��ʾ��������![]() �Ľ⣬Ȼ�����a��x��y�������������ۼ���.
�Ľ⣬Ȼ�����a��x��y�������������ۼ���.
(1)![]()
��-�ڣ���
3y=6��
��y=2��
��y=2����ٵã�
x+4=7��
��x=3��
�������![]() ��
��
��![]() ��
��
�����Ľ�x,y�������ںù�ϵ��.
(2)��������![]() ��
��
![]() ��
��
��5-m=��1��
��m=6��m=4 ��
(3) ![]() ��
��
��+�ڵã�![]() ��
��
��![]() �ۣ�
�ۣ�
�Ѣ۴���ڵ�
![]() ��
��
��![]() ��
��
��a,x,y����������
��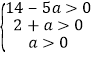 ��
��
��![]() ��
��
�൱a=1ʱ�� x=3��y=4��
��a=2ʱ��x=1��y=3��
��������������������У�ֻ��a=1ʱ��|3-4|=1��
��a=1���÷�����Ľ�x��y�������ںù�ϵ������ʱ������Ľ�Ϊ![]() .
.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��������ѧ�ƻ���֯��������������֯�����˴ӹ�����˾�˽�������Ϣ��
���� |
|
|
�ؿ�������/���� |
|
|
���Ԫ/���� |
|
|
У����ʵ���������,��������![]() ��
��![]() �Ϳͳ���
�Ϳͳ���![]() ������������ò�����
������������ò�����![]() Ԫ��
Ԫ��
��1����ΪУ����ƿ��ܵ��������
��2���ڣ�1���������£�У��������Ը��ԭ��ͳ�Ʒ�����![]() �˲μӣ�����У��Ӧ����������ʡǮ?
�˲μӣ�����У��Ӧ����������ʡǮ?